Городская олимпиада по математике среди физ-мат школАлматы, 2010 год

В треугольнике $ABC$ проведена биссектриса $BK$. Касательная в точке $K$ к окружности $\omega$, описанной около треугольника $ABK$, пересекает сторону $BC$ в точке $L$. Прямая $AL$ пересекает $\omega$ в точке $M$. Докажите, что прямая $BM$ проходит через середину отрезка $ KL$. ( М. Кунгожин )

Комментарий/решение

$\textbf{Определение 1.}$ $ \color{red}{Степенью}$ $\color{red}{точки}$ $M$ $\color{red}{отностительно }$ $\color{red}{окружности}$ $\omega(O,R)$ $\color{blue}{называется}$ $\color{red}{величина}$ $d^2-R^2$ $\color{blue}и$ $\color{blue}{обозначается}$ $\color{blue}{в}$ $\color{blue}{виде}$ $deg_{\omega}M,$ $\color{blue}{где}$ $d=OM.$

$\textbf{Определение 2.}$ $ \color{red}{Радика́льная}$ $ \color{red}{ось}$ $ \color{red}{двух}$ $ \color{red}{окружностей —}$ $\color{blue}{геометрическое}$ $\color{blue}{место}$ $\color{blue}{точек,}$ $\color{blue}{степени}$ $\color{blue}{которых}$ $\color{blue}{относительно}$ $\color{blue}{двух}$ $\color{blue}{заданных}$ $\color{blue}{окружностей}$ $\color{blue}{равны:}$ $deg_{\omega_1}M=deg_{\omega_2}M$

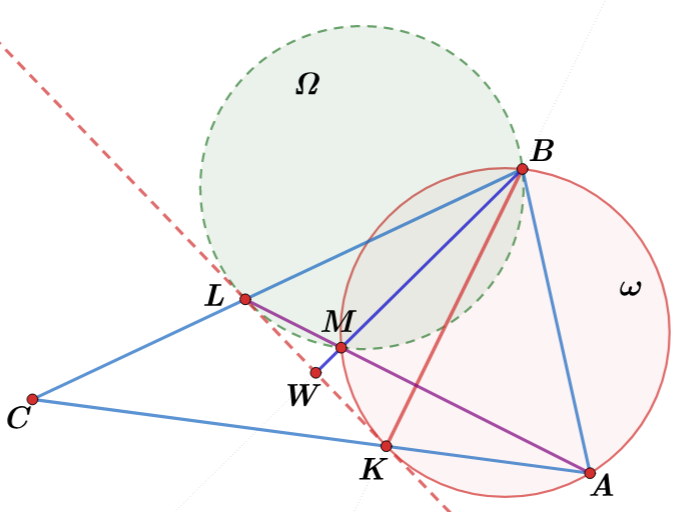
$\color{red}{Доказательство:}$ Пусть $\Omega(I,r)$ - описанная окружность треугольника $LMB.$ Тогда $BM$ - радикальная ось окружностей $\Omega$ и $\omega$.

$$deg_{\omega}W=deg_{\Omega}W \Leftrightarrow OW^2-R^2=IW^2-r^2 \Leftrightarrow LW^2=WK^2 \Leftrightarrow LW=WK$$

По рисунку сверху, докажем что $LW$ касательная, $\angle LKA = 180-\angle LBK$ тогда $\angle ALK = \angle LBK - \angle KBW = \angle LBW$ (из того что $BK $ биссектриса) значит $LW^2=WM \cdot BW = WK^2$