8-я Международная Жаутыковская олимпиада, 2012 год

На диагоналях выпуклого четырехугольника $ABCD$ построены правильные треугольники $ACB'$ и $BDC'$, причем точки $B$ и $B'$ лежат по одну сторону от $AC$, а точки $C$ и $C'$ лежат по одну сторону от $BD$. Найдите $\angle BAD+\angle CDA$, если известно, что $B'C'=AB+CD$.

Комментарий/решение

Пусть $AB∦CD$ и точка $O \in AB \cap CD$, докажем что при таком построений, равенство $AB+CD=B'C'$ будет выполнятся тогда, когда $O \in B'C'$.

1) Пусть $E \in AB' \cap B'C'$ и $F \in B'C \cap C'D$ так же $G \in AC \cap BD$ , тогда $\angle EBG = 180^{\circ}-\angle DB'C = 120^{\circ}$ то есть $AEBG$ вписанный как и $DGCF$ тогда если $O \in B'C'$ получаем что $G \in EF$ так как $\angle B'AO = \angle EAB = \angle EGB = \angle DGF = \angle DCF = \angle B'CO$ откуда $B'OCA$ вписанный, аналогично $DGOC'$ откуда $\angle B'OC + \angle COC' = 120^{\circ}+60^{\circ}=180^{\circ}$ значит $O \in B'C'$.

2) Тогда по (ТЕОРЕМЕ ПОМПЕЮ) для вписанного правильного треугольника $AB'C$ получаем $AO=B'O+OC$ или $AB+BO=B'O+OC$ аналогично и для $DBC'$ получаем $CD+OC = BO+OC'$ откуда суммируя $AB+CD = OC'+OB' = B'C'$.

Значит $\angle AOD = 180^{\circ}-120^{\circ} = 60^{\circ}$ откуда $\angle CDA + \angle BAD = 120^{\circ}$

Построим на $BC$ правильный треугольник $BOC$ во внешнюю сторону. Из $\angle OCB=\angle ACB'=60^{\circ}$ следует $\angle OCB'=\angle ACB$. $\triangle OCB'=\triangle BCA$ поскольку $CB'=AC, CO=CB$. Следовательно $B'O=AB$. Аналогично $C'O=CD$. Поэтому $B'C'=B'O+C'O$, то есть точка $O$ лежит на $B'C'$. Также из равенства треугольников $\angle ABC=\angle COB', \angle DCB=\angle BOC' \Rightarrow\angle ABC+\angle DCB=\angle COB'+\angle BOC'=\angle COB+(\angle BOB'+\angle BOC')=240^{\circ}$.

В четырехугольнике $ABCD$: $\angle BAD+\angle CDA=360^{\circ}-(\angle ABC+\angle DCB)=120^{\circ}$.

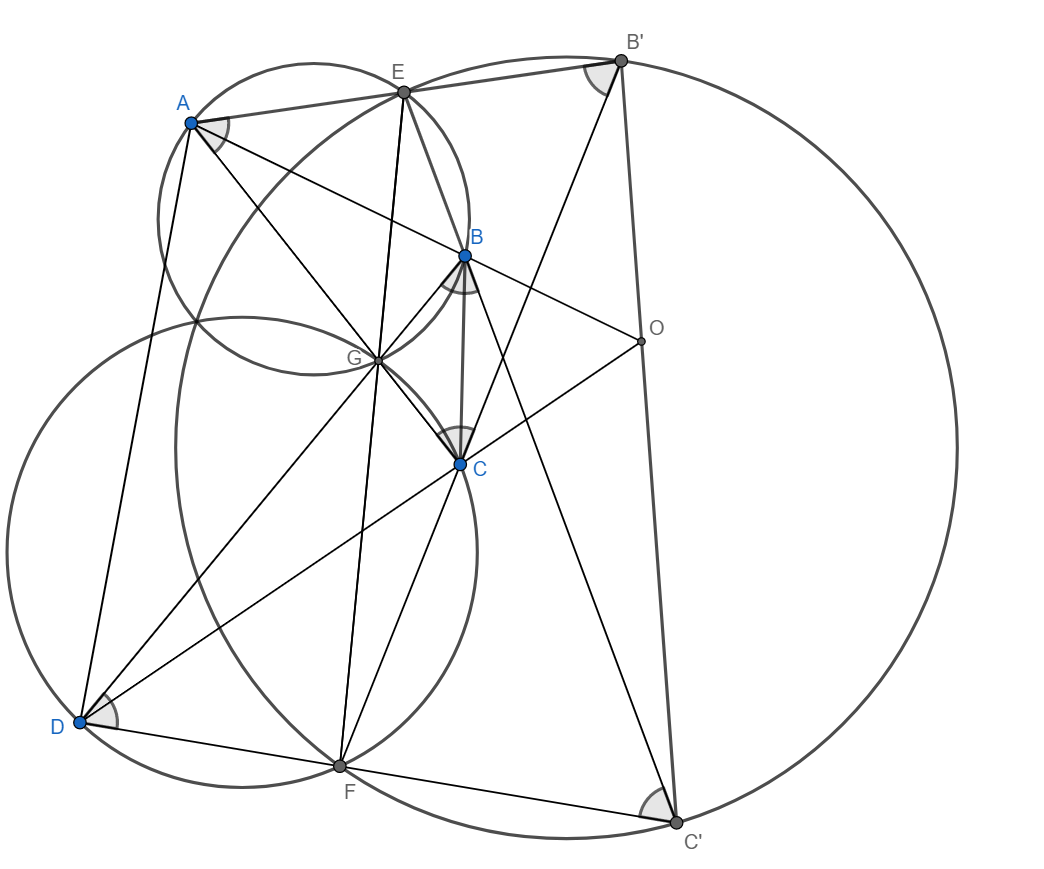
Пусть $AC \cap BD = E, BC' \cap CB' = F, C'B \cap AB' = X, B'C \cap DC' = Y$. Заметим, что из-за равенства нескольких углов, равных $60^\circ$, имеется три вписанных четырехугольника: $AXBE, DYCE, B'C'YX$.

Пусть $\angle AEB = \angle DEC = \varphi$, следовательно, $\angle BXB' = \varphi$. Далее, по теореме синусов:

$\frac{AB}{\sin \varphi} = \frac{XE}{\sin 120^\circ}$, $\frac{CD}{\sin \varphi} = \frac{YE}{\sin 120^\circ}$, $\frac{B'C'}{\sin \varphi} = \frac{XY}{\sin 60^\circ}$.

Из равенства $B'C' = AB + CD$ следует, что

$\frac{XY}{\sin 60^\circ}=\frac{B'C'}{\sin \varphi} = \frac{AB + CD}{\sin \varphi} = \frac{XE + YE}{\sin 120^\circ}$.

Другими словами, $XY=XE+YE$, то есть точки $X, Y, E$ лежат на одной прямой. Следовательно,

$\angle BAD+\angle CDA=(\angle BAE+\angle CDE)+(\angle EAD+\angle EDA)=(\angle BXE+\angle CYE)+(180^\circ-\angle AED)=(180^\circ-\angle BFC)+(180^\circ-\angle BEC)=360^\circ-\angle BFC-\angle BEC=120^\circ$.