Математикадан Эйлер олимпиадасы, 2014-2015 оқу жылы, Дистанциялық кезеңнің 2-ші туры

$ABC$ үшбұрышында $BD$ биссектрисасы, $BDC$ үшбұрышында $DE$ биссектрисасы, ал $DEC$ үшбұрышында $EF$ биссектрисасы жүргізілген. Сонда $BD$ мен $EF$ түзулері параллель болып шыққан. $ABC$ бұрышы $BAC$ бұрышынан екі есе үлкен екенін дәлелдеңіздер.

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Решение. Из условия следует, что $\angle ABD =\angle EBD = \angle CEF = \angle DEF =\angle BDE$. Таким образом, внутренние накрест лежащие углы $ABD$ и $BDE$ при пересечении прямой $BD$ прямыми $AB$ и $DE$ равны. Следовательно, $AB \parallel DE$, откуда $\angle BAC = \angle EDF =\angle EDB =\angle ABD =\angle ABC/2$, что и требовалось доказать.

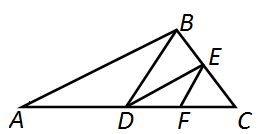
Так как $BD||EF$ значит:

$ \angle BDE=\angle BDE=\angle DEF=\angle FEC $

И по условию:$ \angle ABD=\angle DBC $

Возьмем $ \angle DBC $ как $X$ a угол $ \angle BDE $ как

$Y$. Значит угол $ \angle BED $ Будет $180-X-Y$ а так как угол $ \angle DEC $ $2X$

значит $X=Y$.

Угол $ \angle BDA $ будет $180-2X$ потому что угол $ \angle BDC $ равен $2X$ а так как угол $ \angle ABD $ равен $X$ значит угол $ \angle BAD $ будет равен $X$

А значит угол $ \angle BAC=x $ а $ \angle ABC=2X $