Решения: Олимпиада им. Леонарда Эйлера, Дистанционный этап

Математикадан Эйлер олимпиадасы, 2014-2015 оқу жылы, Дистанциялық кезеңнің 1-ші туры

$n \times n$ квадраттың шаршылары келесі шарт орындалатындай қара және ақ түстерге боялған: екі баған мен екі жолдың қиылысуынан пайда болған төрт шаршылардың ешқайсысы барлығы бір түсті бола алмайды.

$n$ -нің ең үлкен мүмкін мәні қандай?

посмотреть в олимпиаде

Комментарий/решение:

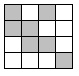
Комментарии от администратора Комментарии от администратора №1. Пример для $n = 4$ показан на рисунке ниже.

Докажем от противного, что квадрат

$5\times 5$ таким способом раскрасить невозможно. Назовем строку преимущественно черной, если в ней черных квадратиков больше, чем белых, и преимущественно белой в противном случае. Из пяти строк найдутся либо три преимущественно черных, либо три преимущественно белых; не умаляя общности будем считать, что нашлись три преимущественно черных строки. В них минимум девять черных клеток.
Теперь рассматриваем только эти три строки. Если в каком-то столбце (назовем его А) стоят три черных клетки, то на оставшиеся четыре столбца приходятся по крайней мере шесть черных клеток. Поэтому найдется столбец (назовем его Б), где есть две черные клетки. Тогда, взяв столбцы А и Б и две строки, в которых находятся две черных клетки столбца Б, получим противоречие.
Значит, в каждом столбце не больше двух черных клеток. Но это возможно только тогда, когда хотя бы в четырех столбцах по две черные клетки. Так как есть только три способа покрасить две клетки из трех в черный цвет, в каких-то двух столбцах раскраска одинакова, и мы снова получаем противоречие.