Математикадан Эйлер олимпиадасы, 2013-2014 оқу жылы, Дистанциялық кезеңнің 4-ші туры


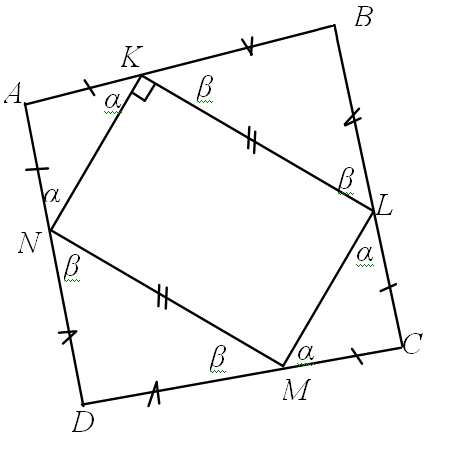
$ABCD$ төртбұрышының $AB$, $BC$, $CD$ және $DA$ қабырғаларынан сәйкесінше $K$, $L$, $M$, $N$ нүктелері алынған. $AK=AN$, $BK=BL$, $CL=CM$, $DM=DN$ және $KLMN$ — тіктөртбұрыш екені белгілі болса, $ABCD$ — ромб екенін дәлелдеңдер.
посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1.     Решение. Треугольники $ANK$, $BKL$, $CLM$ и $DMN$ — равнобедренные по условию. В равнобедренных треугольниках углы при основании равны. Пусть $\angle AKN = \angle ANK =\alpha$, $\angle BKL = \angle BLK = \beta$.

Так как угол $NKL$ прямой, $\alpha+\beta = 90^\circ$. Но $\angle KLB+ \angle MLC = 90^\circ$, значит $\angle MLC = \angle LMC = \alpha$. Аналогично рассуждая, получаем $\angle NMD = \angle MND = \beta$. Поскольку $NK = LM$ как противоположные стороны прямоугольника, треугольники $AKN$ и $CLM$ равны по стороне и двум углам. Аналогично равны треугольники $BKL$ и $DMN$. Тогда $AK = AN = CL = CM$, $BK = BL = DM = DN$, откуда следует, что все стороны четырехугольника $ABCD$ равны.