Математикадан Эйлер олимпиадасы, 2008-2009 оқу жылы, Дистанциялық кезеңнің 4-ші туры

$3\times 3$ тақтаның әр шаршысында натурал саннан жазылған. Онымен қатар барлық сандар бір-бірінен өзгеше және ешқайсысы бірге де, нөлге тең емес. Кез келген шаршыдағы сан оған қабырға бойынша көрші санның бөлгіші екені белгілі. Берілген сандар ішінде ең көп дегенде қанша жай сан болуы мүмкін.

Комментарий/решение

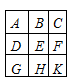
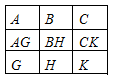
Комментарии от администратора Комментарии от администратора №1.     Ответ. Шесть.
Решение. Докажем, что двумя составными числами обойтись нельзя. Будем рассуждать от противного. Пусть имеется всего два составных числа и 7 простых. Произведение нескольких простых чисел не может делиться на отличное от них простое число. Поэтому составными должны быть: одно из чисел $A$, $B$, $D$; одно из чисел $D$, $G$, $H$; одно из чисел $C$, $E$, $F$, $K$. При этом, чтобы составных чисел было на самом деле всего два, надо, чтобы одним из них было число $D$, а другим — число $F$. Но тогда простое число $H$ оказывается окружёнными тремя простыми числами $E$, $G$, $K$ — противоречие.