Олимпиада имени Леонарда Эйлера2008-2009 учебный год, IV тур дистанционного этапа

В каждой клетке квадрата $3 \times 3$ записано натуральное число. При этом все числа попарно различны и отличны от единицы. Известно, что число, записанное в каждой из клеток, является делителем произведения всех чисел, стоящих в клетках, соседних с ней по стороне. Найдите наибольшее возможное значение количества простых чисел среди выписанных.

Комментарий/решение

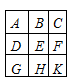
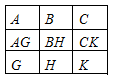
Комментарии от администратора Комментарии от администратора №1.     Ответ. Шесть.
Решение. Докажем, что двумя составными числами обойтись нельзя. Будем рассуждать от противного. Пусть имеется всего два составных числа и 7 простых. Произведение нескольких простых чисел не может делиться на отличное от них простое число. Поэтому составными должны быть: одно из чисел $A$, $B$, $D$; одно из чисел $D$, $G$, $H$; одно из чисел $C$, $E$, $F$, $K$. При этом, чтобы составных чисел было на самом деле всего два, надо, чтобы одним из них было число $D$, а другим — число $F$. Но тогда простое число $H$ оказывается окружёнными тремя простыми числами $E$, $G$, $K$ — противоречие.