Юниорская олимпиада по математике. Районный этап. 2024-2025 учебный год. 8 класс.
Задача №1. Пловец плывет вверх против течения реки. Возле первого моста он потерял пустую флягу. Проплыв еще 20 минут против течения, он заметил свою потерю и вернулся догонять флягу. Догнал он ее возле второго моста. Какова скорость течения реки, если расстояние между мостами равно 2 км?
A) 1,5
B) 1,8
C) 2
D) 2,5
E) 3
комментарий/решение
A) 1,5
B) 1,8
C) 2
D) 2,5
E) 3
комментарий/решение
Задача №2. Найдите количество различных натуральных делителей числа $6^{15} \cdot 2^{17}$.
A) 105
B) 225
C) 2225
D) 2754
E) 2944
комментарий/решение
A) 105
B) 225
C) 2225
D) 2754
E) 2944
комментарий/решение
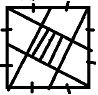
Задача №3. Площадь больщего квадрата 1 м$^2$. Найдите площадь заштрихованного квадратика.
A) $\frac{1}{3}$
B) $\frac{1}{4}$
C) $\frac{1}{5}$
D) $\frac{1}{6}$
E) Анықтау мүмкін емес/ нельзя определить
комментарий/решение
A) $\frac{1}{3}$
B) $\frac{1}{4}$
C) $\frac{1}{5}$
D) $\frac{1}{6}$
E) Анықтау мүмкін емес/ нельзя определить
комментарий/решение
Задача №4. Какую цифру надо вставить вместо $x$, чтобы $567х80$ делилось на 90?
A) 0
B) 2
C) 3
D) 4
E) 1
комментарий/решение(1)
A) 0
B) 2
C) 3
D) 4
E) 1
комментарий/решение(1)
Задача №5. Из операции ниже найдите требуемое значение.
A) $3 \cdot 2^4$
B) $2^{9}$
C) $2^{12}$
D) $2^{20}$
E) $2^{5}$
комментарий/решение
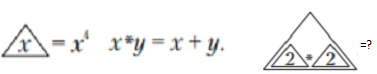
A) $3 \cdot 2^4$
B) $2^{9}$
C) $2^{12}$
D) $2^{20}$
E) $2^{5}$
комментарий/решение
Задача №6. Деревянный кубик с ребром 4 см окрасили в синий цвет, а затем распилили на одинаковые кубики с ребром 1 см. Сколько получилось маленьких кубиков одной синей гранью?
A) 24
B) 6
C) 8
D) 12
E) 36
комментарий/решение
A) 24
B) 6
C) 8
D) 12
E) 36
комментарий/решение
Задача №7. Выпуклом многоугольнике провели все диагонали, их оказалось 44. Сколько сторон у этого многоугольника?
A) 10
B) 12
C) 13
D) 7
E) 11
комментарий/решение
A) 10
B) 12
C) 13
D) 7
E) 11
комментарий/решение
Задача №8. Из них 20 занимаются в математическом кружк, 11 в биологическом кружке и 10 ребят не посещают эти кружки. Сколько биологов увлекается математикой?
A) 2
B) 3
C) 4
D) 5
E) 6
комментарий/решение
A) 2
B) 3
C) 4
D) 5
E) 6
комментарий/решение
Задача №9. Квадрат числа состоит из цифр 0, 2, 3, 5. Найдите сумму цифр этого числа.
A) 5
B) 6
C) 7
D) 8
E) 9
комментарий/решение
A) 5
B) 6
C) 7
D) 8
E) 9
комментарий/решение
Задача №10. Вычислите: $\frac{3}{1 \cdot 2}+\frac{3}{2 \cdot 3}+\frac{3}{3 \cdot 4}+\cdots+\frac{3}{2024 \cdot 2025}.$
A) $\frac{2024}{2025}$
B) $1 \frac{4}{2025}$
C) $1 \frac{624}{675}$
D) $1 \frac{374}{675}$
E) $2 \frac{674}{675}$
комментарий/решение
A) $\frac{2024}{2025}$
B) $1 \frac{4}{2025}$
C) $1 \frac{624}{675}$
D) $1 \frac{374}{675}$
E) $2 \frac{674}{675}$
комментарий/решение
Задача №11. Выполняется равенство $\overline{x x x x}-\overline{y y}=x(\overline{x x})^2$, где $x, y$ цифры. Чему равна сумма $x+y$?
A) 5
B) 11
C) 7
D) 13
E) 9
комментарий/решение
A) 5
B) 11
C) 7
D) 13
E) 9
комментарий/решение
Задача №12. Вычислите: $3 \cdot 6 \cdot 9 \cdot 12 + 81.$
A) 1625
B) 1825
C) 2025
D) 2225
E) 2425
комментарий/решение(1)
A) 1625
B) 1825
C) 2025
D) 2225
E) 2425
комментарий/решение(1)
Задача №13. Если $x y z=1$ то чему равна сумма $\frac{1}{1+x+x y}+\frac{1}{1+y+y z}+\frac{1}{1+z+x z}?$
A) 0,5
B) 2
C) 1
D) 0,8
E) 1,5
комментарий/решение
A) 0,5
B) 2
C) 1
D) 0,8
E) 1,5
комментарий/решение
Задача №14. Всем членам семьи 73 года. Состав семьи муж, жена, дочь и сын. Муж старше жены на 3 года, дочь старше сына на 2 года. Четыре года тому назад всем членам семьи было 58 лет. Сколько лет сейчас сыну?
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
Задача №15. Из трех следующих утверждений два верны, а одно неверно: 1) $A+51$ есть точный квадрат. 2) последняя цифра числа $A$ есть единица. 3) $A-38$ есть точный квадрат. Найдите сумму цифр числа $A$.
A) 21
B) 21
C) 23
D) 24
E) 25
комментарий/решение
A) 21
B) 21
C) 23
D) 24
E) 25
комментарий/решение
Задача №16. Марат пишет целые числа от 1 до 1995. Сколько раз он напишет цифру 0?
A) 199
B) 489
C) 589
D) 169
E) 714
комментарий/решение
A) 199
B) 489
C) 589
D) 169
E) 714
комментарий/решение
Задача №17. Найти разность знаменателя и чиситля дроби. Равную $\frac{399}{1064}$, зная, что сумма числителя и знаменателя составляет куб простого числа.
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
Задача №18. Поезд длиной 1 км медленно движется со скоростью 1 км/час и вползает туннель, длина которого 1км. За сколько времени он полностью пройдет туннель?
A) 1
B) 1 ч 30 мин
C) 2 ч
D) 3 ч
E) 0,5 ч
комментарий/решение
A) 1
B) 1 ч 30 мин
C) 2 ч
D) 3 ч
E) 0,5 ч
комментарий/решение
Задача №19. Какова сумма цифр числа $10^{95}-95$?
A) 839
B) 733
C) 633
D) 842
E) 831
комментарий/решение
A) 839
B) 733
C) 633
D) 842
E) 831
комментарий/решение
Задача №20. Металический диск диаметра 20 см весит 2,4 кг. Из него вырезают диск диаметра 10 см. Сколько весит оставаяся часть?
A) 1,2
B) 1,6
C) 1,8
D) 1,9
E) 2
комментарий/решение
A) 1,2
B) 1,6
C) 1,8
D) 1,9
E) 2
комментарий/решение
Задача №21. Ученик решает задние из 20 задач. За верно решенную задачу ему ставят 8 баллов, за неверно решенную отнимает 5 баллов, за задачу, которую не брался решать 0 баллов. Сколько задач он брался решать, если в сумме он получил 13 баллов.
A) 10
B) 11
C) 12
D) 13
E) 14
комментарий/решение
A) 10
B) 11
C) 12
D) 13
E) 14
комментарий/решение
Задача №22. Сколько всего пар натуральных чисел $(x, y) \in \mathbb{N}$ удовлетворяет условию $2x+1 \vdots y$, $2y+1 \vdots y$?
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
Задача №23. Найдите наименьшее натуральное число, половина которого является точным квадратом, а третья часть — точным кубом.
A) 162
B) 288
C) 648
D) 338
E) 392
комментарий/решение
A) 162
B) 288
C) 648
D) 338
E) 392
комментарий/решение
Задача №24. Студент за 5 лет учебы сдал 31 экзамен. В каждом следующем году он сдавал больше экзаменов, чем в предыдущем. На V курсе экзаменов втрое больше, чем на І курсе, сколько экзаменов на IV курсе.
A) 7
B) 4
C) 5
D) 6
E) 8
комментарий/решение
A) 7
B) 4
C) 5
D) 6
E) 8
комментарий/решение
Задача №25. Сколько натуральных чисел, не делящихся ни на 3, на на 7, ни на 11, имеется среди первых 10000 натуральных чисел?
A) 5105
B) 5205
C) 5305
D) 5405
E) 5505
комментарий/решение
A) 5105
B) 5205
C) 5305
D) 5405
E) 5505
комментарий/решение
Задача №26. У автомобиля новые шины. Шина на заднем колесе выдерживает пробег 16000 км, а на переднем 24000 км. Какой максимальный пробег можно осуществить на этих колесах.
A) 18200
B) 18400
C) 22200
D) 19200
E) 19800
комментарий/решение
A) 18200
B) 18400
C) 22200
D) 19200
E) 19800
комментарий/решение
Задача №27. Отец с двумя сыновями отправились навестить бабушку, которая живет в 33 км от города. У отца есть мотороллер, скорость которого 25 км/ч, а с пассажиром 20 км/ч (двух пассажиров на мотороллере перевозить нельзя). Каждый из братьев идет по дороге со скоростью 5 км/ч. За какое минимальное время все трое доберуться до бабушки?
A) 3
B) 3,5
C) 4,5
D) 5
E) 5,5
комментарий/решение
A) 3
B) 3,5
C) 4,5
D) 5
E) 5,5
комментарий/решение
Задача №28. 625 участников соревнуются в беге. В одном забеге дается старт на пяти дорожках. В каждом забеге определяется 1 победитель, который выходит в следующий тур. Какое общее число забегов необходимо для определения победителя соревнований?
A) 155
B) 106
C) 125
D) 126
E) 156
комментарий/решение
A) 155
B) 106
C) 125
D) 126
E) 156
комментарий/решение
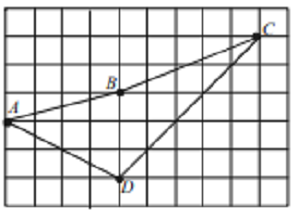
Задача №29. Чему равна площадь $ABCD$, если площадь маленького квадрата принять за 1?
A) 9
B) 10
C) 11
D) 12
E) 13,5
комментарий/решение
A) 9
B) 10
C) 11
D) 12
E) 13,5
комментарий/решение
Задача №30. В треугольнике $ABC$ $\angle C = 58^\circ$. $AK$ и $BM$ высоты треугольника. Какие значения может принимать величина угла между прямыми, содержащими данные высоты?
A) $30^\circ$
B) $45^\circ$
C) $47^\circ$
D) $50^\circ$
E) $58^\circ$
комментарий/решение
A) $30^\circ$
B) $45^\circ$
C) $47^\circ$
D) $50^\circ$
E) $58^\circ$
комментарий/решение