2-я Жаутыковская олимпиада (2006), теоретический тур

(12 баллов)
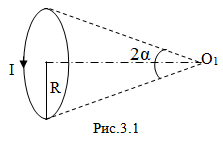
Имеется кольцо радиуса $R$, по которому течет ток $I$.
а) Вычислите магнитное поле в точке $O_1$ на оси кольца. Кольцо видно из точки $O_1$ под углом $2\alpha$. (См.Рис.3.1)

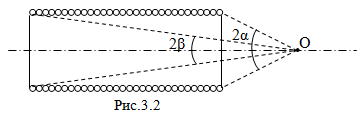
Соленоид с радиусом $R$ состоит из $N$ витков, равномерно намотанных на длине $l$. По соленоиду течет ток $I$.
b) Найдите индукцию магнитного поля на оси соленоида в точке, из которой диаметры торцов видны под углами $2\alpha$ и $2\beta$. (см. Рис.3.2)

В дальнейшем полагаем, что $l>>R$.
с) Вычислите поле $B_0$ внутри соленоида на его оси вдали от торцов;
d) Найдите расстояние $x$, при котором $B=0,1\cdot B_0$ (см. Рис.3.3);

e) Вычислите индуктивность катушки $L$, считая поле внутри катушки вдали от торцов однородным по всему сечению.
Намагниченная пуля пролетает вдоль оси соленоида, подключенного к конденсатору $C$. Магнитный момент пули $M$ параллелен оси соленоида. Будем пренебрегать изменением скорости пули в процессе пролета.
f) Напишите условие того, что время пролета пулей области неоднородности магнитного поля значительно меньше периода колебаний в $LC$ контуре. Считайте в дальнейшем, что это условие всегда выполнено;
g) При какой скорости пули амплитуда колебаний тока в контуре после пролета пули максимальна?
h) Чему при этом равна амплитуда тока $I_{\max}$? Нарисуйте график зависимости $I(t)$ для этого случая.
i) Докажите, что сила, действующая на пулю со стороны магнитного поля, равна $M\frac{ tial B}{ tial x}$ и направлена вдоль оси.
Примечания: Пулю можно рассматривать как кольцо малой площади $S_0$, по которому течет ток $I_0$, причем $M=S_0I_0$.
В теории магнетизма доказывается следующая теорема взаимности: Если поток магнитного поля первого контура через второй обозначить $L_{12}I_1$, а поток поля второго контура через первый обозначить $L_{21}I_2$, то $L_{12}=L_{21}$. При этом предполагается, что знаки потоков согласованы с положительными направлениями обхода контуров.