2-я Жаутыковская олимпиада (2006), теоретический тур

(10 баллов)
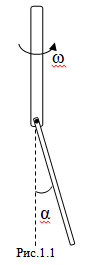
Один из концов однородного массивного стержня длины $L$ шарнирно прикреплен к вертикальной оси. Шарнир устроен так, что в системе отсчета, связанной с осью, стержень может совершать колебания в одной вертикальной плоскости. Трение в шарнире отсутствует. Ось вращается с угловой скоростью $\omega$, ускорение свободного падения — $g$ (Рис.1.1)
a) Вычислите значения угла $\alpha$, при которых этот угол не меняется со временем;
b) Проанализируйте устойчивость системы для каждого равновесного состояния.
Пусть в некоторый момент времени стержень получает небольшое отклонение от устойчивого положения равновесия в разрешенной плоскости.
c) Вычислите период этих колебаний.