1-я международная Иранская олимпиада по геометрии, 2014 год, вторая лига

Точки $P$ и $Q$ выбраны на стороне $BC$ треугольника $ABC$ так, что расстояния от этих точек до середины $BC$ равны. Перпендикуляры к $BC$, восстановленные в точках $P$ и $Q$, пересекают прямые $AC$ и $AB$ в точках $E$ и $F$ соответственно. Прямые $PF$ и $EQ$ пересекаются в точке $M$. Пусть $H_1$ и $H_2$ являются точками пересечения высот треугольников $BFP$ и $CEQ$ соответственно. Докажите, что $AM \perp H_1H_2$.

Комментарий/решение

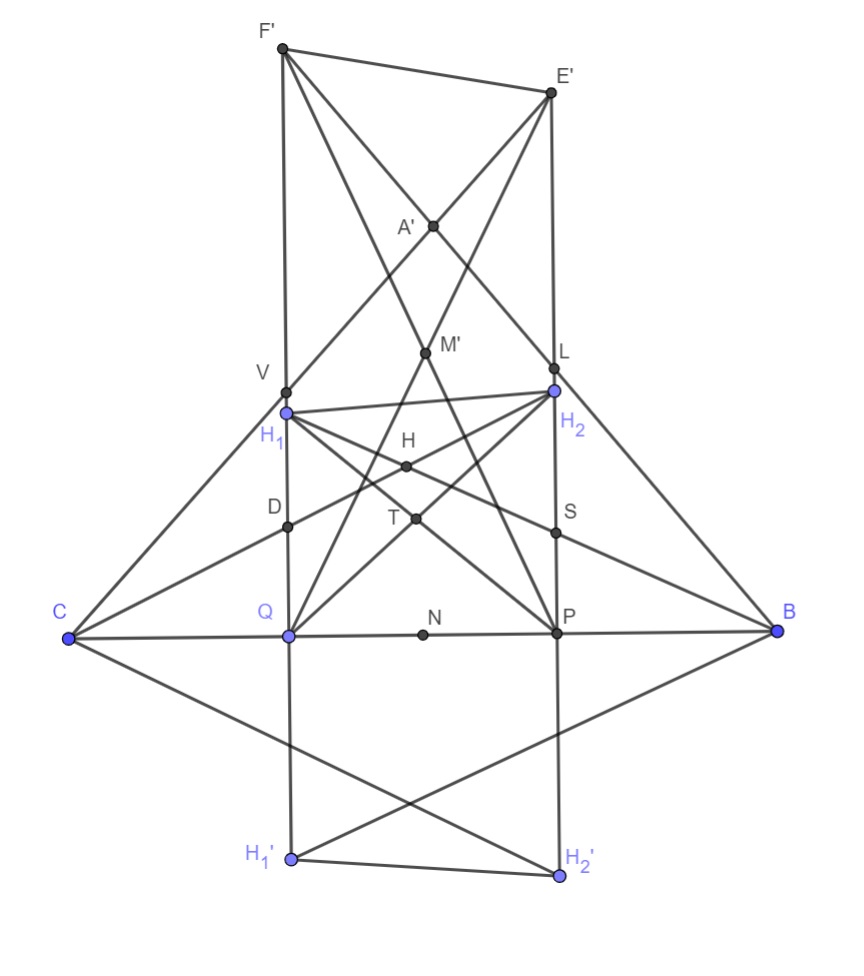
Пусть на отрезке $BC$ выбраны точки $Q,P$ так что $CQ=BP$, пусть $l_{1},l_{2}$ перпендикуляры к $Q,P$ и $H_{1},H_{2}$ произвольные точки на $l_{1},l_{2}$ соответственно, проведем окружность $\omega_{1}, \omega_{2}$ через точки $C,Q,H_{2}$ и $B,P,H_{1}$ соответственно и пусть $E' \in \omega_{1} \cap l_{2}$, $F' \in \omega_{2} \cap l_{1}$ и $A' \in BF' \cap CE'$ и $M' \in QE' \cap PF', \ \ V \in CE' \cap l_{1}, \ \ L \in F'B \cap l_{2},\ D \in CH_{2} \cap l_{1}, \ S \in BH_{1} \cap l_{2}$

Лемма: в данном построении $\angle BH_{1}H_{2} = \angle A'M'F', \ \ \angle CH_{2}H_{1} = \angle A'M'E'$ выполняется $\angle H_{2}TH = \angle F'E'C, \ \ \angle H_{1}TH = \angle E'F'B$

Доказательство: Отметим что из вписанности четырехугольников $F'H_{1}PB, E'H_{2}QC$

$\angle H_{2}H_{1}B+\angle H_{1}H_{2}C = \angle QF'P + \angle QE'P = 180^{\circ} - \angle M'PQ - \angle M'QP = \angle F'M'E'$

Пусть $\angle H_{2}H_{1}B=a, \ \angle H_{1}H_{2}C=b, \ \angle BH_{1}P=x, \ \angle CH_{2}Q=c, \ \angle HTH_{1}=t, \ \angle HTH_{2} =d, \ \angle E'F'B = m, \angle F'E'C = n$ так как по вышеописанному выполняется $t+d=m+n$ покажем что $\dfrac{\sin(d)}{\sin(t)} = \dfrac{\sin(n)}{\sin(m)}$ это и будет значит что $d=n, t=m$

Из теорема Чевы получается: $\dfrac{\sin(d)}{\sin(t)} = \dfrac{\sin(a)}{\sin(x)} \cdot \dfrac{\sin(c)}{\sin(b)}$ из треугольников $H_{1}H_{2}P, \ H_{1}H_{2}Q$ получается $\dfrac{\sin(a)}{\sin(x)} \cdot \dfrac{\sin(c)}{\sin(b)} = \dfrac{H_{2}S}{PS} \cdot \dfrac{QD}{H_{1}D} \cdot \dfrac{H_{1}P}{H_{2}Q}$

из треугольников $F'VE', \ F'LE'$ получается $\dfrac{\sin(n)}{\sin(m)} = \dfrac{F'V \cdot \sin( \angle F'VE')}{E'L \cdot \sin( \angle F'LE')}$ так как $\sin\angle F'VE' = \dfrac{CQ}{CV}, \ \sin \angle F'LE'= \dfrac{BP}{BL}$ то есть

$\dfrac{\sin(n)}{\sin(m)} = \dfrac{F'V}{E'L} \cdot \dfrac{CQ}{CV} \cdot \dfrac{BL}{BP}$

то есть покажем что $$ \dfrac{H_{2}S}{PS} \cdot \dfrac{QD}{H_{1}D} \cdot \dfrac{H_{1}P}{H_{2}Q} = \dfrac{F'V}{E'L} \cdot \dfrac{CQ}{CV} \cdot \dfrac{BL}{BP} \ \ (1)$$

учитывая что $CQ=BP, \ CP=BQ$ тогда $(1)$

$$ \dfrac{H_{2}S}{PS} \cdot \dfrac{QD}{H_{1}D} \cdot \dfrac{H_{1}P}{H_{2}Q} = \dfrac{F'V}{E'L} \cdot \dfrac{ BL}{CV}$$

учитывая что $QH_{1} \cdot QF' = QP \cdot BQ$ и $PH_{2} \cdot PE' = QP \cdot CP$

получается что

$F'V=F'Q-VQ = \dfrac{QP \cdot QB}{H_{1}Q} - \dfrac{CQ \cdot E'P}{CP} =\dfrac{QP \cdot QB}{H_{1}Q} - \dfrac{CQ \cdot PQ}{H_{2}P} = QP \cdot (\dfrac{QB}{H_{1}Q} - \dfrac{QC}{H_{2}P})$

$E'L=PE'-PL = \dfrac{PC \cdot PQ}{H_{2}P} - \dfrac{BP \cdot F'Q}{BQ} = \dfrac{PC \cdot PQ}{H_{2}P} - \dfrac{BP \cdot QP}{H_{1}Q} = QP \cdot (\dfrac{PC}{H_{2}P} - \dfrac{BP}{H_{1}Q})$

$PS = \dfrac{BP \cdot H_{1}Q}{QB}$ и $QD = \dfrac{CQ \cdot H_{2}P}{QB}$

$H_{2}S = H_{2}P-PS = H_{2}P - \dfrac{CQ \cdot H_{1}Q}{QB} = \dfrac{H_{2}P \cdot QB-CQ \cdot H_{1}Q}{QB}$

$H_{1}D = H_{1}Q-QD = H_{1}Q - \dfrac{CQ \cdot H_{2}P}{QB} = \dfrac{H_{1}Q \cdot QB-CQ \cdot H_{2}P}{QB}$

так же $ \dfrac{BL}{CV} = \dfrac{H_{2}P}{H_{2}Q} \cdot \dfrac{H_{1}P}{H_{1}Q}$

подставляя в $(1)$ учитывая что $\dfrac{QD}{PS} = \dfrac{H_{2}P}{H_{2}Q}$

$$\dfrac{BL}{CV} = \dfrac{H_{2}P}{H_{2}Q} \cdot \dfrac{H_{1}P}{H_{1}Q}$$

из вписанности двух четырехугольников по условию, получается

$$\dfrac{H_{2}P}{H_{2}Q} \cdot \dfrac{H_{1}P}{H_{1}Q} = \dfrac{CP}{CE'} \cdot \dfrac{F'B}{BQ} = \dfrac{F'B}{CE'}$$

что верно так как $ \dfrac{BL}{F'B} = \dfrac{CV}{CE'} = \dfrac{BP}{BQ} $

Решение: Пусть $H_{1}', H_{2}'$ симметричные точкам $H_{1},H_{2}$ относительно $BC$ тогда $\angle QF'F = \angle H_{1}BC = \angle CBH_{1}'$ тогда $F'P \perp BH_{1}$ аналогично $E'Q \perp CH_{2}'$ из леммы $\angle A'M'F' = \angle BH_{1}H_{2} = \angle BH_{1}'H_{2}$ откуда заменяя $M'=M$, $H_{1}=H_{1}', \ H_{2}=H_{2}'$ получается $AM \perp H_{1}H_{2}$