Олимпиада имени Леонарда Эйлера2008-2009 учебный год, III тур дистанционного этапа

Две биссектрисы треугольника пересекаются под углом 60 градусов. Докажите, что один из углов этого треугольника равен 60 градусам.

Комментарий/решение

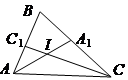
Комментарии от администратора Комментарии от администратора №1.     Решение. Пусть биссектрисы $AA_1$ и $CC_1$ треугольника $ABC$ пересекаются в точке $I$. Допустим, что $\angle AIC_1 = 60^\circ$. По теореме о внешнем угле треугольника $\angle AIC_1 = \angle IAC + \angle ICA = ( \angle BAC + \angle BCA)/2$, откуда $\angle BAC + \angle BCA = 120^\circ$ и $\angle ABC = 180^\circ - \angle BAC - \angle BCA = 60^\circ$. Но это ещё не всё решение: ведь может случиться, что $\angle AIC = 60^\circ$. Однако, тогда $\angle IAC + \angle ICA = 120^\circ$, откуда $\angle BAC + \angle BCA = 240^\circ$, что невозможно.