Международный математический турнир городов — Астана и Алматы (11 октября)

Жариялау күні: 2015-10-09

Уважаемые школьники и учителя! Казахстанский филиал МГУ имени М.В.Ломоносова (на базе ЕНУ имени Л.Н.Гумилева) приглашает Вас принять участие в Международной математической олимпиаде 37-й «ТУРНИР ГОРОДОВ».

Турнир городов состоит из 2 туров: весенний и осенний. Каждый из них делится на базовый и основной вариант. В этом году базовый вариант пройдет 11 октября 2015 г., основной вариант 25 октября 2015 г. Школьники выпускных классов, показавшие очень высокие результаты, приглашаются на финальный устный тур в Москве в марте-апреле 2016г. Победителям и призерам финального тура предоставляются льготы при поступлении в российские ВУЗы.

В олимпиаде могут принять участие школьники 8-11 классов. Школьники будут разделены на 2 лиги: старшая (10-11) и младшая (8-9).

Каждая задача Турнира городов оценивается некоторым количеством баллов, которое указывается в листке с заданием. За частичное решение задачи начисляется меньшее количество баллов. Итог подводится по трем задачам, по которым достигнуты наилучшие результаты; баллы за пункты одной задачи суммируются.

Просьба ознакомиться с задачами прошлых лет. При себе иметь 12-листовую тетрадь в клетку и письменные принадлежности. По желанию можно взять питье и шоколадку.

Рассадка начнется в 9:00. Олимпиада начнется в 10:00. Олимпиада завершится в 15:00.

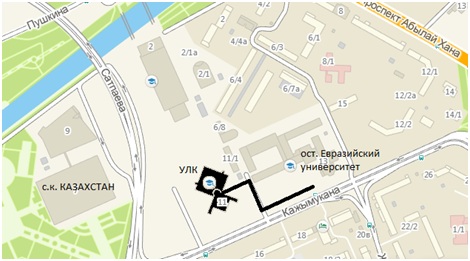
Место проведения: учебно-лабораторный корпус ЕНУ имени Гумилева (на карте темным цветом). Находится через дорогу от спорт комплекса Казахстан.
Автобусы: 3, 25, 28, 48 (ближняя остановка), 14, 18, 23, 31, 40, 73 (остановка через дорогу).

Олимпиаду по городу Астана проводит:
Баев Ален Жуматаевич, преподаватель КФ МГУ, 87071850464, a-l-e-n@mail.ru,
Центр олимпийской подготовки «Аль-Фараби», 87071189432.

 

Участие в олимпиаде бесплатно! Но обязательна предварительная регистрация!

Образец заявки для школ. Заявку нужно отправить на электронный адрес a-l-e-n@mail.ru.

Форма самостоятельной регистрации.

 Подробности проведения турнира по городу Алматы смотрите здесь.

Комментарий(0)