Международная олимпиада 2023, Чиба, Япония, 2023 год
Есеп №1. Келесі қасиетке ие барлық $n>1$ құрама натурал сандарын табыңыз: егер $d_1, d_2, \ldots, d_k$ арқылы $n$-ның барлық натурал бөлгіштерін белгілесек, мұнда $1=d_1 < d_2 < \ldots < d_k=n $, онда кез келген $1 \leqslant i \leqslant k-2$ үшін $d_i$ саны $d_{i+1}+d_{i+2}$ санын бөледі.
комментарий/решение(6)
комментарий/решение(6)
Есеп №2. Сүйірбұрышты $ABC$ үшбұрышы ($AB < AC$) $\Omega$ шеңберіне іштей сызылған. $S$ нүктесі $\Omega$-ның $CAB$ доғасының ортасы. $A$ арқылы өтетін және $BC$ қабырғасына перпендикуляр $BS$ кесіндісін $D$, ал $\Omega$-ны екінші рет $E \neq A$ нүктесінде қияды. $D$ арқылы өтетін және $BC$-ға параллель түзу $BE$ түзуін $L$ нүктесінде қиып өтеді. $BDL$ үшбұрышына сырттай сызылған шеңберді $\omega$ деп белгілейік. $\omega$ мен $\Omega$ шеңберлері екінші рет $P$ нүктесінде қиылысын. $\omega$-ға $P$ нүктесінде жүргізілген жанама түзу $BS$-пен қиылысқанда, сол қиылысу нүктесі $\angle BAC$ биссектрисасында жатқанын дәлелдеңіздер.
комментарий/решение(3)
комментарий/решение(3)
Есеп №3. $k \geqslant 2$ натурал саны берілген. Келесі қасиетке ие барлық $a_1, a_2, \ldots$ натурал сандарының барлық шексіз тізбегін табыңыз: теріс емес бүтін коэффициенттері $c_0, c_1, \ldots, c_{k-1}$ бар әрі барлық натурал $n \geq 1$ үшін $$P\left(a_n\right)=a_{ n+1} a_{ n+2} \cdots a_{n+k}$$ болатындай $$P(x)=x^k+c_{k-1} x^{k-1}+\cdots+c_1 x+c_0$$ түріндегі $P$ көпмүшесі табылады.
комментарий/решение(5)
комментарий/решение(5)
Есеп №4. Ешбір екеуі өзара тең емес оң нақты $x_1, x_2, \ldots, x_{2023}$ сандары берілген. Кез келген $n=1,2, \ldots, 2023$ үшін $$a_n=\sqrt{\left(x_1+x_2+\cdots+x_n\right)\left(\frac {1) }{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n}\right)}$$ саны бүтін сан екені белгілі. $a_{2023} \geqslant 3034$ екенін дәлелдеңіз.
комментарий/решение(2)
комментарий/решение(2)
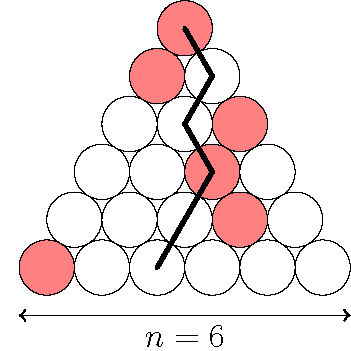
Есеп №5. $n \geq 1$ натурал сан болсын. Жапон үшбұрышы деп жалпы $1+2+\cdots+n$ бірдей дөңгелектерден құралған, әрбір $i=1,2, \ldots, n$ үшін нөмірі $i$ болатын қатарда дәл $i$ дөңгелегі бар, ал әр қатарда дәл бір дөңгелек қызыл түске боялған тең бүйірлі үшбұрыш түрінде салынған фигураны айтамыз. Жапон үшбұрышындағы ниндзя жолы деп аталатын $n$ дөңгелек тізбегі келесідей құрастырылған: 1-ші қатардағы дөңгелектен бастаймыз, содан кейін кезекпен төменгі бір дөңгелекке түсеміз, сосын оның астындағы екі дөңгелектің біріне жылжи бере, $n$-ші қатарға жету жол. Төменде $n=6$ үшін жапондық үшбұрыштың мысалы, сондай-ақ екі қызыл дөңгелектен тұратын ниндзя жолы берілген. Кез келген жапон үшбұрышында кем дегенде $k$ қызыл дөңгелегі бар ниндзя жолы болатындай ең үлкен $k$ санын ($n$-ға байланысты) табыңыз.
комментарий/решение(4)
комментарий/решение(4)
Есеп №6. Тең қабырғалы $ABC$ үшбұрышы берілген. $A_1, B_1, C_1$ нүктелері $ABC$-ның ішінде $B A_1=A_1C, $ $CB_1=B_1A, $ $AC_1=C_1B$ және $$\angle BA_1 C+\angle CB_1 A+\angle AC_1B=480^{\circ} $$ болатындай етіп таңдалады. $B C_1$ және $C B_1$ түзулері $A_2$, $AC_1$ және $CA_1$ түзулері $B_2$, ал $AB_1$ және $BA_1$ түзулері $C_2$ нүктесінде қиылысады. $A_1B_1C_1$ үшбұрышы теңбүйірлі емес екені белгілі. $A_1A_2,$ $BB_1B_2$ және $CC_1C_2$ үшбұрыштарына сырттай сызылған үш шеңберлер қандай да ортақ екі нүкте арқылы өтетінін дәлелдеңіздер.
комментарий/решение(5)
комментарий/решение(5)