Математикадан облыстық олимпиада, 2011-2012 оқу жылы, 11 сынып

Тікбұрышты емес $ABC$ үшбұрышының бұрыштары $\text{tg}A\cdot \text{tg}B\cdot \text{tg}C=\left[ \text{tg}A \right]+\left[ \text{tg}B \right]+\left[ \text{tg}C \right]$ теңдігін қанағаттандыратын болса, осы үшбұрыштың ең кіші бұрышын табыңдар. Мұнда арқылы $x$ санының бүтін бөлігі, яғни $x$-тан аспайтын ең үлкен бүтін сан белгіленген.

Комментарий/решение

Ответ :$45^\circ$

Решение : Легко видеть, что $1*2*3=[1]+[2]+[3] $ . Отсюда следует, что если найдутся такие углы $A, B, C $, что $A+B+C=180$[1] и $tg A=1;tg B=2;tg C=3$, то условие задачи выполняется и наименьший угол будет равен $arctg 1=45^\circ $. Построим треугольник

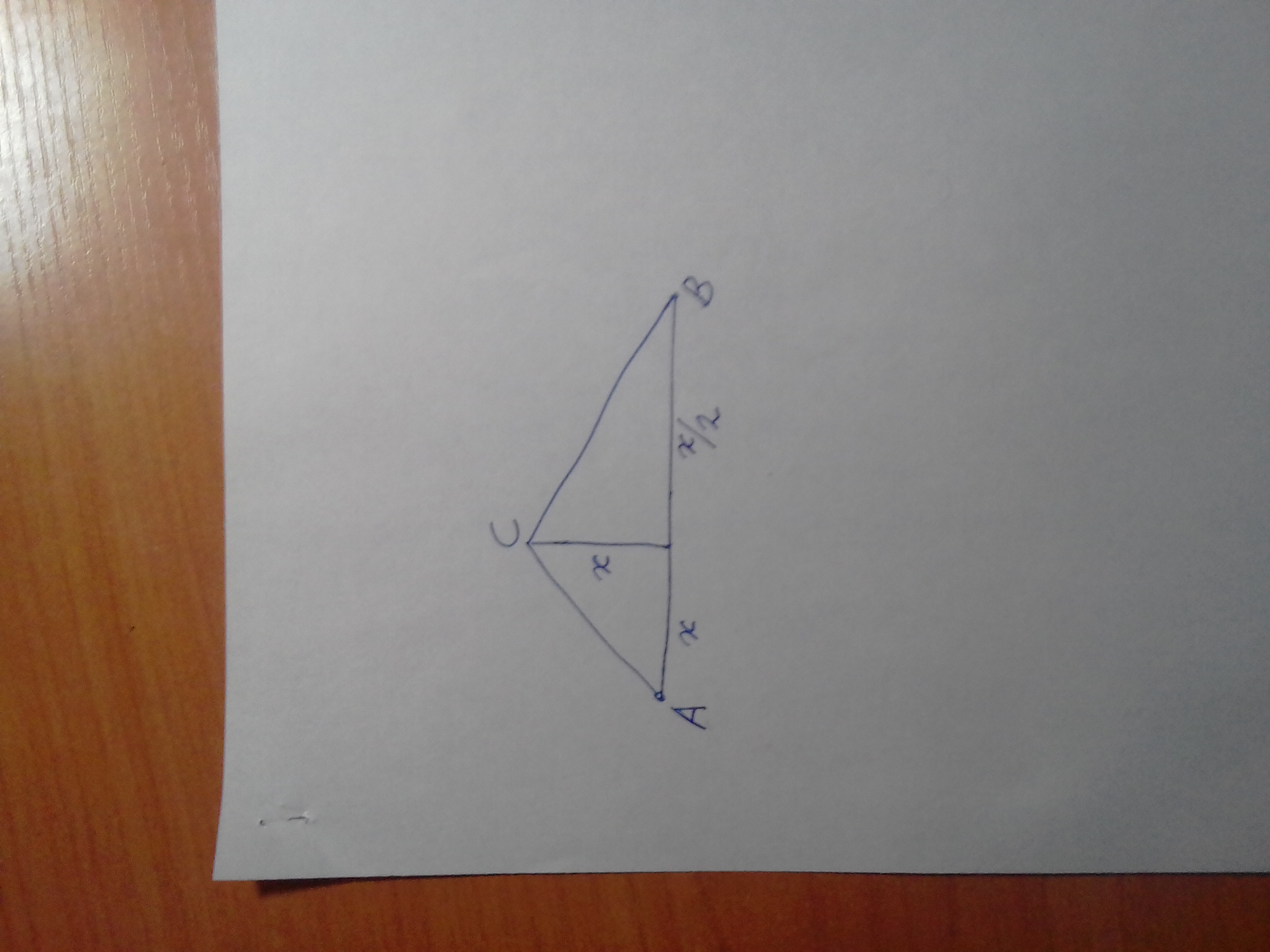
Имеем $ tg C=\dfrac {1+\dfrac{1}{2}}{1-1*\dfrac {1}{2}}=3$ . Отсюда следует верность утверждения [1] и правильность решения задачи

Найдено еще несколько решений

$\angle A=45^{\circ};\angle B=22,5^{\circ};\angle C=112,5^{\circ};$-точное решение

Решения с точностью до $1\cdot{10^{-6}}$

$$\angle A=45^{\circ};\angle B=29,316511^{\circ};\angle C=105,683489^{\circ};$$

$$\angle A=45^{\circ};\angle B=32,852405^{\circ};\angle C=102,147595^{\circ};$$

$$\angle A=45^{\circ};\angle B=35,052045^{\circ};\angle C=99,947955^{\circ};$$

$$\angle A=45^{\circ};\angle B=36,562753^{\circ};\angle C=98,437247^{\circ};$$

$$\angle A=45^{\circ};\angle B=37,668208^{\circ};\angle C=97,331792^{\circ};$$

Я думаю смысла нет в решение этой задачу с помощью приблизительных ответов.

Я решал это численными методами. Это тоже правильное решение. Невязка не превысила $10^{-6}$.

Вот нормальное решение:

$Ответ: 45^\circ$

Заметим что $tgA •tgB•tgC=tgA+tgB+tgC$. Тогда $tgA+tgB+tgC=[tgA]+[tgB]+[tgC]$, но так как $[x]\leq x$, $tgA,tgB,tgC$ являются целыми. Обозначим их через $x,y,z$. Тогда достаточно решить уравнение $xyz=x+y+z$. Это уравнение симметрична, пусть $z \leq y \leq x$. Используя что $x(yz-1)=y+z$, можем найти что при $3 \leq yz$ решений нет( так как $(3-1)x>y+z)$, и что при $yz \leq -1$ тоже нет решений (так как $z<0<y \leq x$ и $y+z=x(yz-1) \leq -2x <z<z+y$). Дальше мы понимаем что $0 \leq yz \leq 2$, перебором понимаем что только при $(x,y,z)=(3,2,1) и (0,a,-a)$ имеет решение. Так как тангенс угла треугольника не может быть равным $0$, значит что только первая тройка подходит. Значит ответ: $arctg(1)=45^\circ$

Я не придираюсь, просто интересно, как получен переход от $tg A\cdot tg B \cdot tg C=[tg A]+[tg B]+[tg C]$ к $tg A\cdot tg B \cdot tg C=tg A+tg B+tg C$?

$tg A\cdot tg B \cdot tg C=tg A+tg B+tg C$ это тождество, которое выполняется для углов любого треугольника (можете это сами доказать через формулы, либо посмотреть доказательство в интернете), поэтому решение пользователя abensad верно.

Также ваш ответ $\angle A=45^{\circ};\angle B=22,5^{\circ};\angle C=112,5^{\circ};$ неверен (можно проверить на калькуляторе)

Спасибо за Ваши разъяснения, Abensad, Ereb. 15. По крайней мере, теперь я разобрался с решением данной задачи. Лично для меня тема с этой задачей закрыта.

Вы правильно делаете, всегда спрашивайте критикуйте, может быть я ошибаюсь. Только с помощью спор и можем сделать этот сайт лучше.

Цитирую Вас:"...$tg A,tg B,tg C$ являются целыми.". Численное решение дало огромное количество корней, при котором $tg A,tg B,tg C$ не являются целыми по отдельности. Тем не менее, эти корни в точности выполняют условие задачи. Мной были получены разнообразные углы в диапазоне от 10 до 60 градусов с точностью до 6 знака