Городская Жаутыковская олимпиада по математике, 8 класс, 2018 год

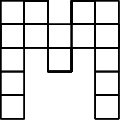
Задача №1.  На сколько частей можно разрезать фигуру на рисунке ниже так, чтобы все части были одинаковыми? Укажите всевозможные варианты. (Две фигурки считаются одинаковыми, если одна из них может быть получена из другой поворачиванием или (и) переворачиванием. Резать можно только по линиям сетки.)

комментарий/решение

---

Задача №2.  Докажите, что при любых целых нечетных значениях $a,$ $b$ и $c$ выражение $ab(a-b)+bc(b-c)+ca(c-a)$ кратно 16.
комментарий/решение(3)

---

Задача №3.  В выпуклом четырехугольнике $ABCD$ известно: $\angle ABC=140^\circ$, $\angle ADC=115^\circ$, $\angle CBD=40^\circ$, $\angle CDB=65^\circ$. Вычислите угол $\angle ACD$.
комментарий/решение(1)

---

Задача №4.  Существует ли натуральное число $n > 1$ такое, что $ 2^n > n^{2018}$? Ответ обоснуйте.
комментарий/решение(1)

---

Задача №5.  В окружности проведено
а) 20 хорд;
б) 19 хорд.
Никакие три хорды не пересекаются в одной точке и никакие две хорды не имеют общего конца. Отметим все точки пересечения хорд. Могло ли оказаться так, что отмеченными окажутся ровно 100 точек?
комментарий/решение

---

Задача №6.  Среди чисел $a,$ $b$ и $c$ произведение любых двух не равно третьему числу. Если $a+b+c=1$, то докажите равенство: $$\left( {\frac{1}{{a - bc}} + \frac{1}{{b - ac}} + \frac{1}{{c - ab}}} \right)\left( {a - bc} \right)\left( {b - ac} \right)\left( {c - ab} \right) = 4abc.$$
комментарий/решение(1)

---

Задача №7.  Докажите, что существует 2018 последовательных натуральных чисел, среди которых ровно 25 чисел являются точными квадратами.
комментарий/решение(1)

---

Задача №8.  Даны три концентрические окружности радиусов 3, 4 и 5. Пересекающиеся хорды $AB$ и $CD$ окружности радиуса 5 касаются окружностей радиусов 3 и 4 соответственно. Докажите, что прямые $AC$ и $BD$ пересекаются под прямым углом.
комментарий/решение(3)

---