Математикадан республикалық олимпиада, 2008-2009 оқу жылы, 10 сынып

$ABC$ үшбұрышында іштей сызылған шеңбер $BC$, $CA$ және $AB$ қабырғаларын сәйкесінше $A_1$, $B_1$ және $C_1$ нүктелерінде жанап өтеді. $A_1C_1B_1$ үшбұрышының ортоцентрін $H_1$ деп белгілейік. $ABC$ үшбұрышының іштей сызылған шеңбер центрін $I$, ал сырттай сызылған шеңбер центрін $O$ деп белгілесек, онда $I$, $O$ және $H_1$ нүктелері бір түзудің бойында жататынын дәлелдеңіз.

Комментарий/решение

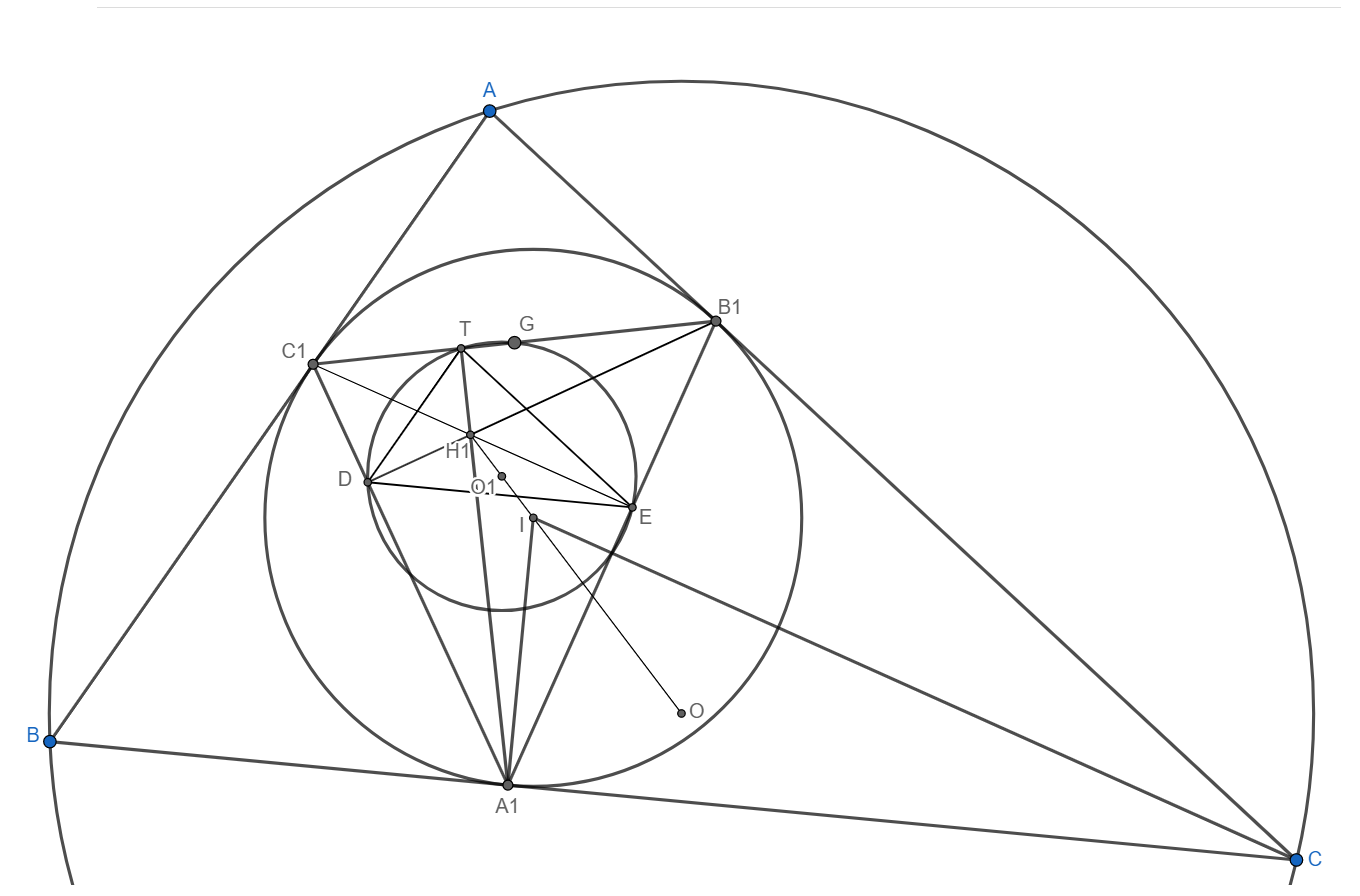
Пусть $A_{1}T, \ B_{1}D, \ C_{1}E$ - высоты треугольника $A_{1}C_{1}B_{1}$, точки $D,T,E$ лежат на одной окружности в силу окружности девяти точек, пусть $O_{1}$ центр этой окружности, по известному утверждению $O_{1}$ лежит в середине отрезка $H_{1}I$ (прямая Эйлера).

1)$\angle H_{1}DT = \angle H_{1}CT = 90-\angle C_{1}B_{1}A_{1}=90-\dfrac{180 - \angle ABC}{2} = \dfrac{\angle ABC}{2}$ и

$\angle H_{1}DE = \angle H_{1}A_{1}E = 90-\angle C_{1}B_{1}A_{1} = \dfrac{\angle ABC}{2}$.

Откуда $\angle TDE = \angle ABC$ аналогично и с остальными углами треугольника $TDE$, получаем что $TD || AB, \ TE || AC, \ DE || BC$.

Пусть $R,r$ - радиусы вписанной и описанной окружностей треугольника $ABC$.

2)Докажем что $\dfrac{IO_{1}}{IO} = \dfrac{r}{R}$(1) используя то что $IO=\sqrt{R^2-2Rr}$ (теорема Эйлера) или через $H_{1}I=2IO_{1}$ получим $H_{1}I = r\sqrt{1-\dfrac{2r}{R}}=r \sqrt{2cos(A+B)-2cosA-2cosB+3}(2)$.

Если $G$ середина $B_{1}C_{1}$ тогда $A_{1}H_{1}=2IG=2r \cdot sin(\dfrac{A}{2})$ и $\angle H_{1}A_{1}I = \dfrac{A+2B-\pi}{2}$ тогда из треугольника $H_{1}A_{1}I$ по теореме косинусов получим $(2)$ значит верно и $(1)$.

3) Если $A',B',C'$ симметричные точки относительно $O$, то при гомотетии с центром $(I, -\dfrac{R}{R_{TDE}})$ окружность описанная около треугольника $TDE$ перейдет в описанную окружность $ABC$, а сам треугольник $TDE$ в $A'B'C'$ и $O_{1}$ в $O$ значит $O,I,O_{1},H$ лежат на одной прямой.

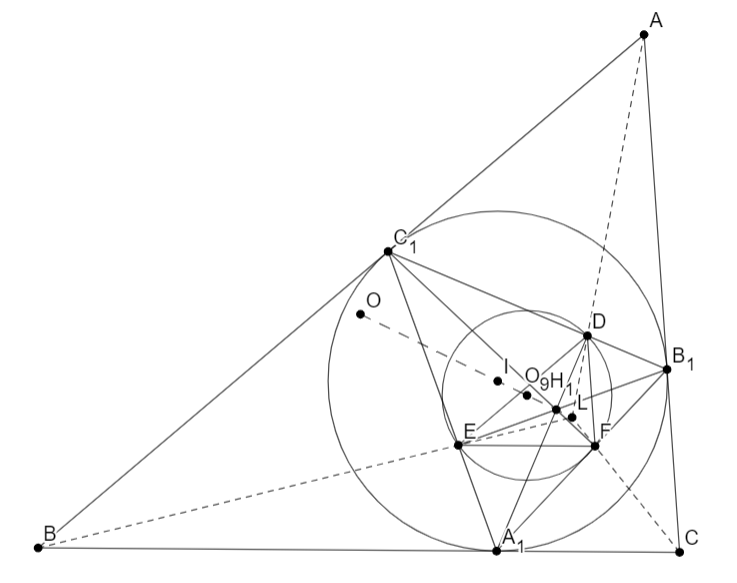
$D,E,F$ - основания высот треугольника $A_1B_1C_1$ из $A_1,B_1,C_1$ соответственно. Тогда:

$A)$ $H_1$ - инцентр $DEF$.

$B)$ окружность $(DEF)$ - окружность девяти точек $A_1B_1C_1$ с центром $O_9$, который лежит на прямой Эйлера $A_1B_1C_1$, то есть прямой $IH_1$.

$C)$ $DEF$ и $ABC$ гомотетичны относительно $L$ - точки пересечения $AD,BE,CF$ (известное свойство). Иначе говоря $L \in IH_1$.

Из этого всего следует, что при гомотетии с центром $L$ и коэффициентом $\frac{LA}{LD}$: $H_1 \to I, O_9 \to O$. То есть $O,I,O_9,H_1,L$ - лежат на одной прямой.