XIV математическая олимпиада «Шелковый путь», 2020 год
Жазықтықтағы шекті $X$ нүктелер жиынының дөңес қабықшасы деп кемінде бір $X$-тің төбелерінен құрылған дөңес көпбұрышының ішінде немесе қабырғаларында орналасқан нүктелер жиынын айтамыз (нүкте немесе кесінді дөңес көпбұрыш деп саналады. Дөңес көпбұрыштың кез келген үш төбесі бір түзудің бойында жатпайды және дөңес көпбұрыш өзінің шекарасын қамтиды). ( Зиманов А. )
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1. Напомним теорему Хелли: если в конечном множестве выпуклых множеств точек на плоскости каждые три пересекаются, то и все пересекаются.
Докажем, что $n = 9m$ подходит. Пусть $X$ — произвольное множество из $9m$ различных точек на плоскости, а $Y$ — множество подмножеств $X$ размера $6m + 1$.
Предположим, что существуют такие $A, B, C \in Y$, что их пересечение пусто. Пронумеруем все точки из $X$ числами от 1 до $9m$. Выпишем на листе бумаги сначала все номера точек из множества $A$, затем из множества $B$ и в конце из множества $C$. В итоге, мы выпишем $|A| + |B| + |C| = 18m + 3$ числа. Так как эти три множества не пересекаются, то мы не могли выписать никакое число более, чем два раза. Значит, мы выписали не более $2 \cdot 9m = 18m$ чисел — противоречие. Следовательно, любые три элемента $Y$ пересекаются.
Так как выпуклая оболочка множества точек полностью содержит это множество, то выпуклые оболочки любых трех элементов $Y$ пересекаются. Следовательно, по теореме Хелли, выпуклые оболочки всех элементов $Y$ имеют какую-то общую точку $O$.
Докажем следующую лемму: если выпуклая оболочка какого-то конечного множества точек $Z$ содержит какую-то точку $P$, то существует $W \subseteq Z$, такое что $|W| \leq 3$ и выпуклая оболочка $W$ содержит $P$. По определению выпуклой оболочки, существует выпуклый многоугольник с множеством вершин $V \subseteq Z$ (возможно, вырожденный), который содержит эту точку $P$. Если $|V| \leq 3$, то $V$ подходит в качестве $W$. Иначе, сделаем произвольную триангуляцию многоугольника с вершинами в $V$. Точка $P$ должна лежать хотя бы в одном треугольнике разбиения. Множество вершин такого треугольника подходит в качестве $W$.
Заведем мешок, в который будем складировать непустые подмножества $X$. Определим следующую операцию, изменяющую $X$ и $Y$: выберем любое $A \in Y$. Так как выпуклая оболочка $A$ содержит $O$, то, по лемме, существует такое $B \subseteq A$, что $|B| \leq 3$ и выпуклая оболочка $B$ содержит $O$. Положим $B$ в мешок (очевидно, $B$ непусто), удалим элементы $B$ из $X$, и удалим из $Y$ множества, содержащие элементы $B$.
После одной операции мощность $X$ уменьшается не более, чем на три, и $Y$ непусто до тех пор, пока $|X| \geq 6m + 1$. Следовательно, мы можем выполнить операцию хотя бы $m$ раз. Выполним операцию ровно $m$ раз. Оставшиеся в $X$ точки распределим произвольным образом между множествами в мешке.
Итак, множества в мешке составляют разбиение начального множества точек на $m$ множеств и выпуклая оболочка каждого из них содержит точку $O$, т. е. они пересекаются, что нам и было нужно.
Комментарии от администратора Комментарии от администратора №2. Индукцией по $m$ докажем, что любые хотя бы $4m^2$ различных точек на плоскости можно разбить на $m$ непустых множеств, выпуклые оболочки которых пересекаются. При $m = 1$ утверждение, очевидно, верно. Пусть оно верно для $m = k - 1$, где $k \geq 2$. Докажем, что оно верно и для $m = k$. Рассмотрим произвольное множество $X$ из хотя бы $4k^2$ различных точек на плоскости. Пусть $Y$ — подмножество точек $X$, лежащих на границе выпуклой оболочки всех точек из $X$. Если $|Y| < 4k$, то $|X \setminus Y| > 4k^2 - 4k > 4(k-1)^2$. По предположению индукции, $X \setminus Y$ можно разбить на $k - 1$ непустое множество точек, выпуклые оболочки которых пересекаются. Если добавить $Y$ к этому $k - 1$ множеству, то мы получим $k$ множеств, выпуклые оболочки которых пересекаются (так как выпуклая оболочка $Y$ содержит все точки из $X \setminus Y$). Если же $|Y| \geq 4k$, то рассмотрим два случая. Если все точки из $Y$ лежат на одной прямой, то и все точки из $X$ лежат на одной прямой. Проведем вдоль этой прямой ось координат и обозначим точки из $X$ через $A_1, A_2, \ldots, A_{|X|}$ по возрастанию координат. Так как $4k^2 > 2k$, то нам подходит разбиение: \[X = \{A_1, A_{|X|}\} \cup \{A_2, A_{|X|-1}\} \cup \ldots \cup \{A_{k-1}, A_{|X|-k+2}\} \cup \{A_k, A_{k+1}, \ldots, A_{|X|-k+1}\}.\] Иначе, точки $Y$ лежат на границе какого-то невырожденного выпуклого многоугольника. Обозначим точки из $Y$ в порядке обхода по часовой стрелке границы этого многоугольника через \[A_1, A_2, \ldots, A_k, B_k, B_{k-1}, \ldots, B_1, C_1, C_2, \ldots, C_k, D_k, D_{k-1}, \ldots, D_1, E_1, E_2, \ldots, E_{|Y| - 4k}.\] Пусть \[Z = \{A_k, B_k, C_k, D_k, E_1, \ldots, E_{|Y| - 4k}\} \cup (X \setminus Y).\] Докажем, что нам подходит следующее разбиение: \[X = \left(\bigcup_{i=1}^{k-1} \{A_i, B_i, C_i, D_i\}\right) \cup Z.\] Для этого достаточно доказать ключевое утверждение: выпуклые оболочки множеств \[\{A_1, B_1, C_1, D_1\}, \{A_2, B_2, C_2, D_2\}, \ldots, \{A_k, B_k, C_k, D_k\}.\] пересекаются. Через $f(M)$ будем обозначать выпуклую оболочку множества точек $M$. Пусть \[T \in A_1B_1 \cap A_kD_k,\] \[H_i = f(\{A_1, A_2, \ldots, A_i, B_i, B_{i-1}, \ldots, B_1, C_1, C_2, \ldots, C_i, D_i, D_{i-1}, \ldots, D_1\})\] и \[V_i = f(\{A_i, A_{i+1}, \ldots, A_k, B_k, B_{k-1}, \ldots, B_i, C_i, C_{i+1}, \ldots, C_k, D_k, D_{k-1}, \ldots, D_i\}).\] Тогда для любого $1 \leq i \leq k$ верно \[T \in A_1B_1 \subseteq H_i \ \text{и} \ T \in A_kD_k \subseteq V_i.\] Следовательно, \[T \in \bigcap_{i=1}^{k} (H_i \cap V_i) = \bigcap_{i=1}^{k} f(\{A_i, B_i, C_i, D_i\}),\] что и требовалось доказать.
Докажем, что $n=m\cdot 2^{m+1}$ подходит. Рассмотрим множество $S$ из $n$ точек. Очевидно, достаточно найти хотя бы $m$ непустых, попарно непересекающихся подмножества $S,$ выпуклые оболочки которых будут иметь общую точку.
Через $f(M)$ будем обозначать выпуклую оболочку множества точек $M.$
Шаг 1. “Сведем” задачу к выпуклому многоугольнику.
Пусть $V_1$ множество вершин $f(S)$ (берем только вершины этого выпуклого многоугольника). Аналогично определим $V_{i+1}$ для $f(S/ V_i).$ По итогу получим разбиение $S$ на непустые множества $V_1,…,V_k,$ причем
$$f(V_k)\subset f(V_{k-1}) \subset \ldots f(V_{1}).$$
Если $k \ge m,$ то требуемое разбиение найдено, иначе $\exists i: |V_i|>\dfrac{n}{m}=2^{m+1},$ выберем $X\subset V_i,$ что $|X|=2^{m+1}.$ Отметим, что точки этого множества образуют выпуклый многоугольник.
Шаг 2: Докажем индукцией по $m$, что $X$ можно разбить на $m$ множеств требуемым образом.
База для $m=1$ очевидна, для $m=2$ достаточно найти два отрезка (концы которых лежат в $S$) с общей точкой.
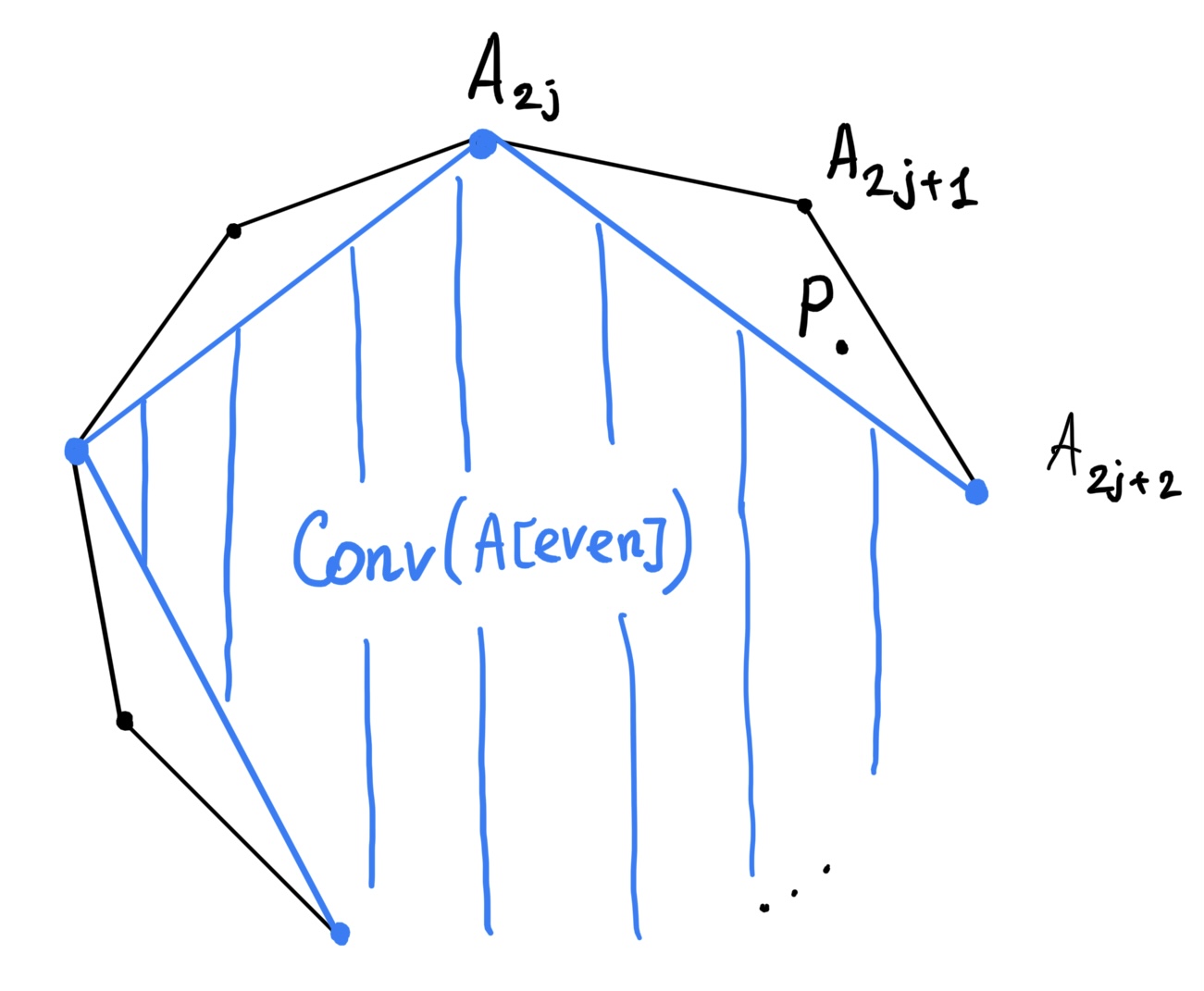
Допустим утверждение верно для $m-1\ge 2.$ Пусть $X$ образует многоугольник $A_1A_2\ldots A_{2^{m+1}}.$ Пусть $A[odd]=\{A_1,A_3,...,A_{2^{m+1}-1} \}, A[even]=\{ A_2,A_4,\ldots, A_{2^{m+1}} \}$
По предположению $A[odd]$ можно разбить на $m-1$ множеств, что $\exists P$ которая принадлежит выпуклой оболочке каждого $\Rightarrow P\in f (A[odd])\subset f(X).$
Достаточно доказать, что $P\in f ( A[even] ).$ Допустим обратное, тогда $P\in f (X/ A[even]) ,$ откуда $P\in f \{ (A_{2j},A_{2j+1},A_{2j+2} \} )$ для некоторого $j.$
В разбиений $A[odd]$ есть множество не содержащее $A_{2j+1},$ тогда $f$ от этого множества
$$\subset f (A[odd]/ \{A_{2j+1} \} )\subset f(X/ \{ A_{2j},A_{2j+1},A_{2j+2} \} ) \implies P\in f(X/ \{A_{2j},A_{2j+1},A_{2j+2} \} )$$
но точки из $f(X/ \{ A_{2j},A_{2j+1},A_{2j+2} \} )$ лежат по другую сторону от точки $P$ относительно прямой $A_{2j}A_{2j+2}.$ Противоречие.
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.