Математикадан облыстық олимпиада, 1998-1999 оқу жылы, 10 сынып

$O$ нүктесі — $ABC$ үшбұрышының $A$ төбесіне сәйкес келетін іштейсырт $\omega$ шеңберінің центрі ($AB\ne AC$). $\omega$ шеңбері $BC$ кесіндісін $K$ нүктеде, ал $AC$ және $AB$ түзулерінің созындыларын сәйкесінше $M$ және $P$ нүктелерінде жанайды. $AO$ және $PM$ түзулері $T$ нүктесінде қиылысады, ал $AK$ түзуі $\omega$ шеңберін екінші рет $H$ нүктесінде қияды. $K$, $T$, $O$ және $H$ нүктелерінің бір шеңбердің бойында жататынын дәлелдеңіздер.

Комментарий/решение

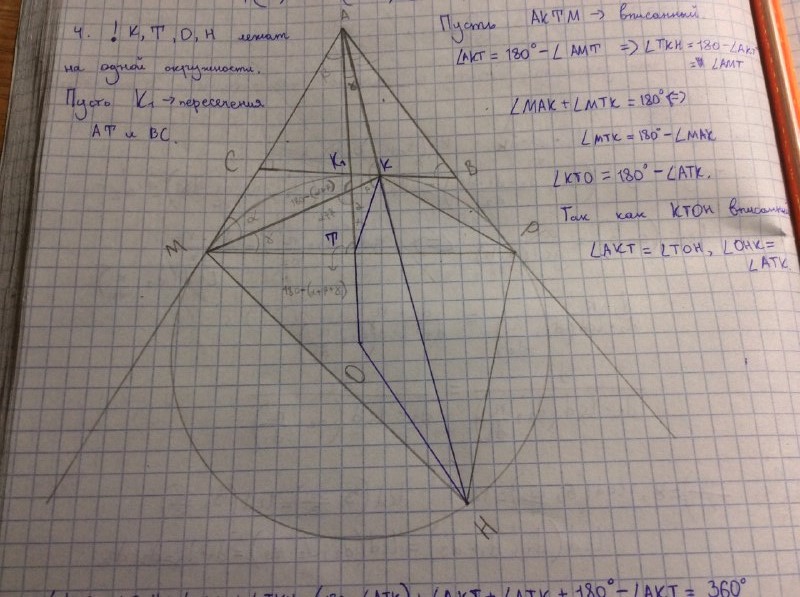
Пусть $ \square AKTM$ вписанный (можно заметить через равенство углов). Тогда $$\angle AKT=180^\circ - \angle AMT$$$$ \Rightarrow \angle TKH = 180^\circ - \angle AKT = \angle AMT.$$

$$\angle MTK = 180^\circ - \angle MAK $$. Так как $ \square KTOH$ вписанный, $$\angle AKT = \angle TOH, \angle OHK =\angle ATK $$. Тогда нам достаточно доказать, что сумма четырёхугольника $\square KTOH$ равен $360^\circ$

$$\angle KTO +\angle TOH + \angle OHK +\angle TKH = (180^\circ - \angle ATK) + \angle AKT +\angle ATK + (180^\circ - \angle AKT) = 360^\circ $$

Я новичок в инверсии, так что строго не судите и скажите, если решение некорректна. Заметим, что PA и MA касательные к $\omega$. Сделаем инверсию относительно $\omega$. Тогда точка T перейдет в A. K и H остаются на своем месте. O перейдет в точку на бесконечности, а оно лежит на линии KH. Значит, образ KH переходит в окружность, проходящую через K, T, O, H.

Абсолютно верно, только есть одна поправочка. Точка O остаётся на месте если вы делаете инверсию относительно окружности $\omega$ . Да вы правильно указали, что точка $A$ перейдет в точку $T$. Тогда прямая $KH$ перейдет в окружность$(KOH)$. В силу того, что $KH$ проходит через $A$, то $T$ будет лежать на окружности $(KOH)$.