Олимпиада Туймаада по математике. Младшая лига. 2018 год

Окружность касается стороны $AB$ треугольника $ABC$ в точке $A$, стороны $BC$ — в точке $P$ и пересекает сторону $AC$ в точке $Q$. Прямая, симметричная $PQ$ относительно $AC$, пересекает прямую $AP$ в точке $X$. Докажите, что $PC=CX$. ( С. Берлов )

Комментарий/решение

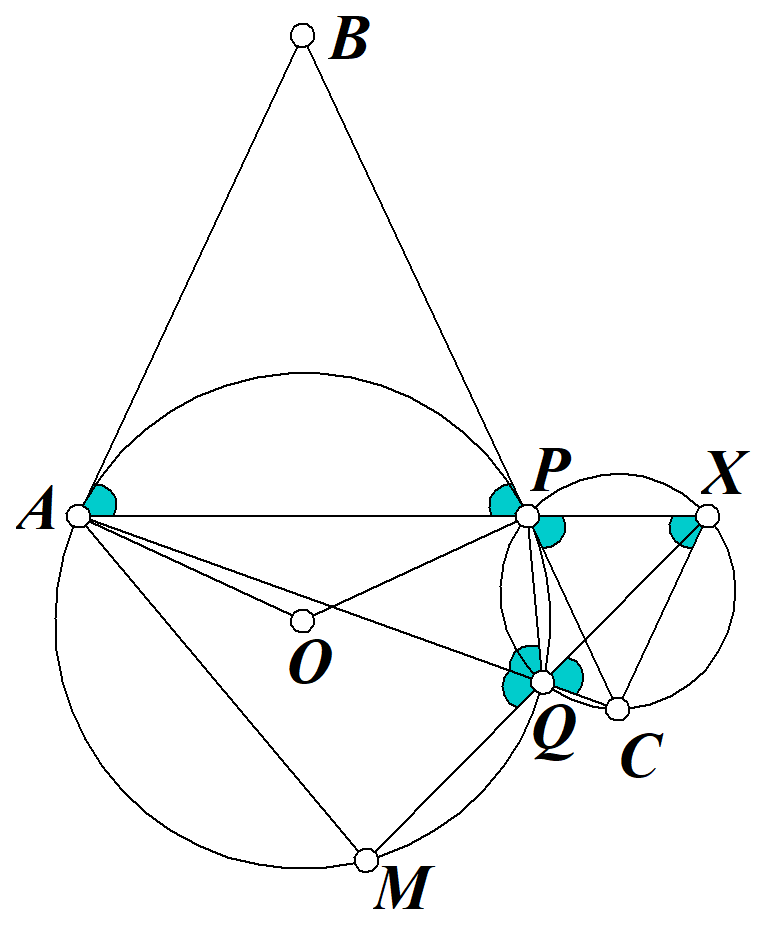
1) $AB$ и $BC$ касаются окружности, поэтому $OA\bot AB;OP\bot BP$

2) $\triangle BAO=\triangle BPO\rightarrow BA=AP$

3) $\triangle BAP-$ равнобедренный (следует из $(2)$), значит $\angle BAP=\angle BPA$

4) $\angle BPA=\angle XPC$ как вертикальные

5) Рассмотрим четырёхугольник $ABPO$. Сумма углов в нем равна $360^{\circ}$

$\angle OAP+\angle ABP+\angle BPO+\angle POA=360^{\circ}$

6) $\angle OAP+\angle BPO=90^{\circ}+90^{\circ}=180^{\circ}$ (следует из $(1)$)

7) Из $(5,6)$ следует, что $\angle ABP+\angle POA=180^{\circ}\rightarrow \angle POA=180^{\circ}-\angle ABP$

8) $\angle POA$ и $\angle PQA$ опираются на одну дугу окружности, но при этом $\angle POA-$ центральный, а $\angle PQA-$ вписанный $\rightarrow \angle PQA=\dfrac{\angle POA}{2}=\dfrac{180^{\circ}-\angle ABP}{2}=90^{\circ}-\dfrac{\angle ABP}{2}=\angle BPA$

9) В силу симметрии $PQ$ и $QM$ относительно $AC$ имеем $\angle PQA=\angle MQA$

10) Обобщая $(9,8,7,3,4)$,имеем $\angle BAP=\angle BPA=\angle XPC=\angle PQA=\angle MQA$

11) $\angle MQA=\angle XQC$ как вертикальные

12)Так как $\angle XPC=\angle XQC$,и опираются на один отрезок $XC$ ,то вокруг $PXCQ-$ можно описать окружность

13) Из $(12)$ следует $\angle PQX=\angle PCX$ как опирающиеся на одну дугу $PX$

14) $\angle PCX=\angle PQX=180^{\circ}-\angle PQA-\angle XQC=180^{\circ}-\angle BAP-\angle BPA=\angle ABP$

15) Из $(14)$ и $(4)$ следует подобие $\triangle ABP\sim\triangle PCX\rightarrow \angle CPX=\angle CXP\rightarrow PC=CX$

Обозначим точку симметричную $P$ относительно $AC$ как $P'$ и окружность касающуюся сторону $BC$ в точке $P$ и сторону $AB$ в точке $A$ как $\omega$

Получается: $$\angle PQA=\angle P'QA=\angle CQX$$

Так как $BC$- касательная к окружности $\omega$: $$\angle PQA=\angle BPA=\angle CPX$$

Следовательно $PQCX$-вписанный и следовательно: $$\angle PQA=\angle CXP=\angle CPX$$

Получается $PC=CX$, ч.т.д.