14-я Международная Жаутыковская олимпиада, 2018 год


На сторонах $AB$, $BC$ и $CA$ треугольника $ABC$ соответственно взяты точки $N$, $K$ и $L$ так, что $AL=BK$ и $CN$ -- биссектриса угла $C$. Отрезки $AK$ и $BL$ пересекаются в точке $P$. Обозначим через $I$ и $J$ центры вписанных окружностей треугольников $APL$ и $BPK$ соответственно. Пусть $Q$ -- точка пересечения прямых $CN$ и $IJ$. Докажите, что $IP=JQ$. ( М. Кунгожин )
посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1.     Если $CA=CB$, то задача очевидна. Если $CA \ne CB$, то без потери общности можем предположить, что $CN$ пересекает отрезок $PK$.

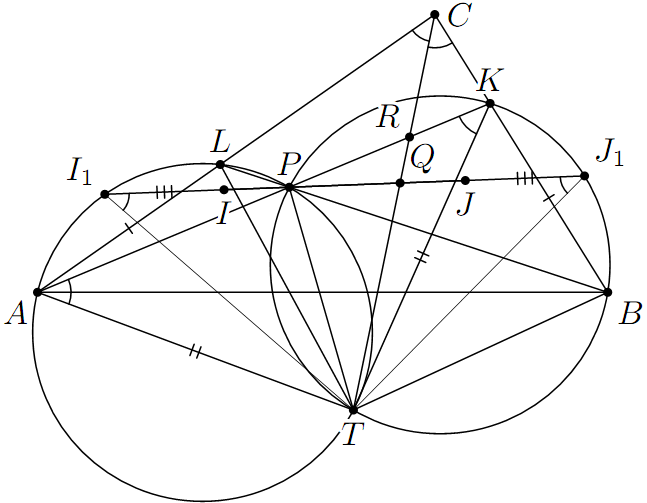
Пусть описанные окружности $\omega_1$ и $\omega_2$, соответственно треугольников $APL$ и $BPK$, во второй раз пересеклись в точке $T$. Тогда $$\angle LAT=\angle TPB=\angle TKB.\quad (1)$$ и $\angle ALT=\angle APT=\angle TBK$, то есть $\triangle ALT= \triangle KBT$, откуда $$AT=TK.\quad (2)$$ Из (1) также следует, что четырехугольник $ACKT$ вписанный, а из (2), что $\angle ACT=\angle TCK$, то есть $T$ лежит на биссектрисе $CN$.
Пусть $IJ$ пересекает $\omega_1$ и $\omega_2$ в точках $I_1$ и $J_1$ соответственно. Так как радиусы окружностей $\omega_1$ и $\omega_2$ равны и $AL=BK$, равны и треугольники $ALI_1$ и $BKJ_1$. Воспользуемся леммой Мансиона: середина дуги $XY$ окружности, описанной около треугольника $XYZ$, находится на равных расстояниях от концов этой дуги и центра вписанной окружности этого треугольника. По этой лемме $I_1I=I_1L=J_1K=J_1J$. Кроме того, $\angle PI_1T=\angle PAT=\angle PKT=\angle PJ_1T$, следовательно, $I_1T=J_1T$. Таким образом, $T$ лежит и на серединном перпендикуляре к отрезку $I_1J_1$, и на серединном перпендикуляре к отрезку $IJ$.
Осталось доказать, что $T$ лежит на серединном перпендикуляре к отрезку $PQ$. Пусть $R=AK \cap CT$. Тогда $\angle PRT = \angle ART=\angle RAC+\angle ACR=\angle RAC+\angle AKT=\angle RAC+\angle KAT= \angle LAT=\angle BPT$. Так как $PQ$ делит угол $RPB$ пополам, $\angle PQT=\angle PRT+\angle RPQ= \angle BPT+\angle RPQ= \angle BPT+\angle QPB =\angle QPT$, следовательно, $T$ лежит на серединном перпендикуляре отрезка $PQ$. Поэтому $IP=JQ$.

  0
2018-02-06 23:00:11.0 #

Опечатка в последнем $\angle PRT = \angle ART = \angle BPT \ne \angle PBT$

Matov