Математикадан «Туймаада» олимпиадасы. Жоғары лига. 2017 жыл

$ABCD$ тіктөртбұрышының $AD$ қабырғасының созындысында, $D$ нүктесінен кейін $E$ нүктесі белгіленді. $EC$ сәулесі, $ABE$ үшбұрышына сырттай сызылған $\omega $ шеңберін екінші рет $F$ нүктесінде қияды. $DC$ және $AF$ сәулелері $P$ нүктесінде қиылысады. $E$ нүктесі арқылы өтетін $\ell $ түзуіне, $AF$ түзуіне параллель $CH$ перпендикуляры салынды. $PH$ түзуі $\omega $ шеңберімен жанасатынын дәлелдеңіз. ( А. Кузнецов )

Комментарий/решение

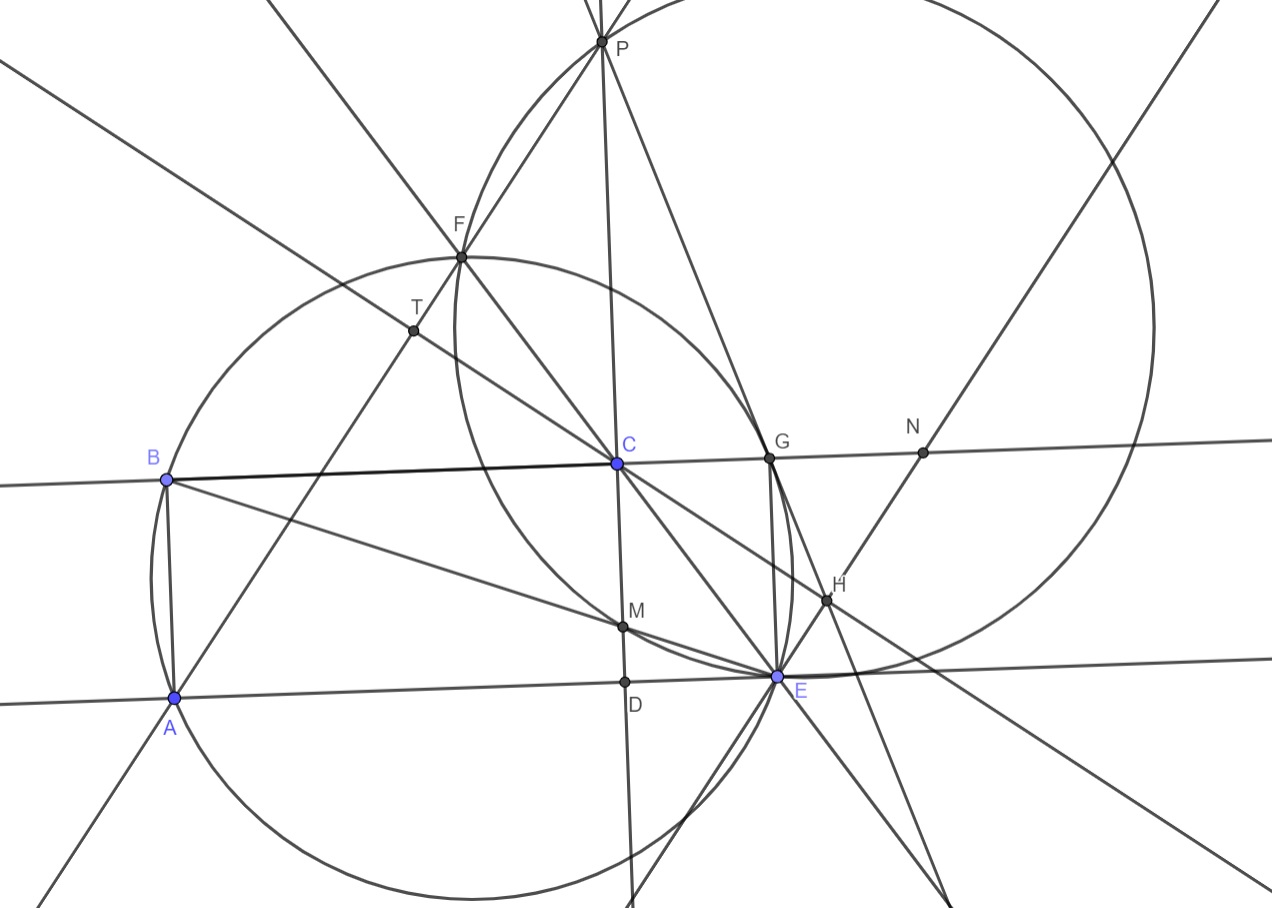
Пусть $G \in BC \cap \omega$ и $ M \in CD \cap BE$ тогда так как $\angle APD = \angle PAB = \angle FEB$ и так как $l || AF$ тогда $\angle APD = \angle GEN$ откуда $FPEM$ вписанный , тогда $PC \cdot CM = CE \cdot CF$ но $BC \cdot CG = CE \cdot CF$ то есть $ PC \cdot CM = BC \cdot CG$ то есть $BPGM$ вписанный , тогда $\angle PGB = \angle PMB = \angle GEB$ то есть $PG$ касательная, так как $CH \perp \ l$ тогда $DCGHE$ вписанный , откуда тогда $\angle HGN = \angle EN = \angle BEG = \angle BMP = \angle BGP$ то есть $P,G,H$ лежат на одной прямой.