58-я Международная Математическая OлимпиадаБразилия, Рио-де-Жанейро, 2017 год

Пусть $R$ и $S$ — две различные точки на окружности $\Omega$ такие, что $RS$ не является диаметром. Пусть $\ell$ — касательная к $\Omega$ в точке $R$. Точка $T$ выбрана так, что $S$ является серединой отрезка $RT$. Точка $J$ выбрана на меньшей дуге $RS$ окружности $\Omega$ так, что окружность $\Gamma$, описанная около треугольника $JST$, пересекает $\ell$ в двух различных точках. Пусть $A$ — та из общих точек $\Gamma$ и $\ell$, которая находится ближе к точке $R$. Прямая $AJ$ вторично Пересекает $\Omega$ в точке $K$. Докажите, что прямая $KT$ касается $\Gamma$.

Комментарий/решение

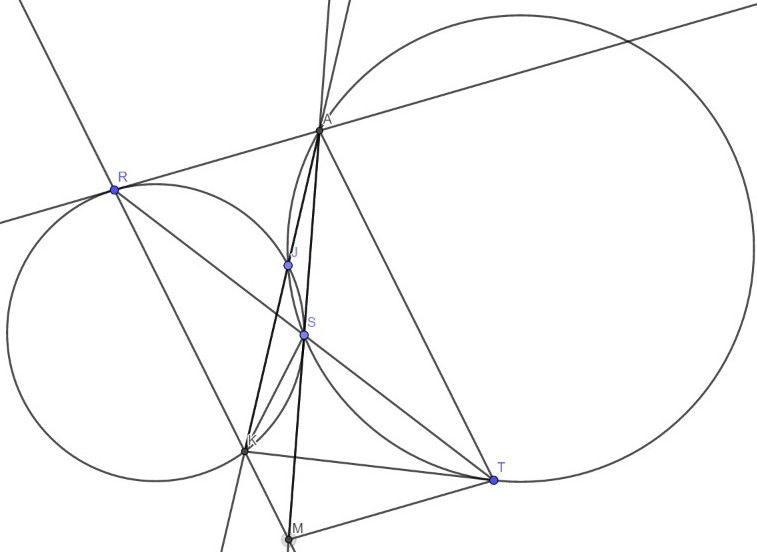
$AS \cap RK = M$

$\angle SRK = \angle KJS = \angle STA \Rightarrow RK \parallel AD$

$RS = ST, RK \parallel AD \Rightarrow ARTM - паралеограмм$ $\Rightarrow \angle STM = \angle SRA$ $(1),$ $\angle KMS = \angle SAT$ $(2)$

$AR$ $касается$ $\Omega \Rightarrow \angle SKR = \angle SRA$ $(3)$

$(1) + (3):$ $\angle SKR = \angle STM \Rightarrow STMK - вписанный$ $\Rightarrow$

$\Rightarrow \angle KMS = \angle KTS$ $(4)$

$(2)+(4):$ $\angle SAT = \angle KTS \Rightarrow KT$ $касается$ $\Gamma$ в точке $T.$ $#$

Лемма: $AT \parallel RK$.

Доказательство: имеем $\angle{JAT} = 180^{\circ} - \angle{JST} = \angle{JSR} = \angle{JKR}$, из чего следует желаемый вывод.

Теперь предположим, что описанная окружность треугольника $SKT$ снова пересекает $RK$ в точке $X$. Я утверждаю, что $X,S,A$ коллинеарны. Чтобы доказать это, мы вместо этого покажем, что $RXTA$ — параллелограмм; мы уже знаем, что $RX \parallel TA$, поэтому теперь достаточно показать, что $RA \parallel XT$. Но это следует из $\angle{STX} = \angle{SKX} = \angle{ART}$, причем доказательство в других конфигурациях проводится аналогичным образом.

Таким образом, $\angle{KTR} = \angle{RXA} = \angle{SAT}$, подразумевая, что $KT$ касается $\Omega$, и мы закончили.