Эйлер атындағы олимпиада, 2010-2011 оқу жылы, аймақтық кезеңнің 1 туры

$8 \times 8$ шахмат тақтасы шаршыларының центрлері арқылы өзін өзі қимайтындай тұйықталған сызық жүргізілген. Әрбір буын көршілес горизонталь, вертикаль не диоганаль шаршылардың центрлерін қосады. Сызық қоршаған бөліктегі қара бөліктің ауданы ақ бөліктің ауданына тең болатынын дәлелдеңіз. ( Д. Храмцов )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Решение 1. Проведём пунктиром вертикальные и горизонтальные линии через центры клеток доски. На получившейся пунктирной сетке каждое звено нашей ломаной соединяет узлы, соседние по вертикали, горизонтали или диагонали. Поэтому пунктирные прямые разбивают область, ограниченную ломаной, на единичные квадратики и половинки квадратиков, получаемые разрезанием их по диагонали. Осталось заметить, что в каждом таком квадратике и в каждом таком треугольнике площади чёрной и белой частей равны. Действительно, каждый квадратик содержит по две четверти клеток обоих цветов, а треугольник — четверть клетки одного цвета и два треугольничка, каждый из которых составляет восьмую часть клетки другого цвета.

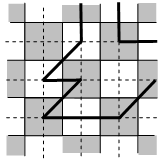
Комментарии от администратора Комментарии от администратора №2.     Решение 2. Рассмотрим новую квадратную сетку, образованную вертикальными и горизонтальные линиями, проходящими через центры клеток доски. Каждый квадрат этой сетки разрежем диагоналями на четыре треугольника. Очевидно, каждый получившийся треугольник наполовину белый, а наполовину — черный. С другой стороны, фигура, ограниченная ломаной, состоит из таких треугольников, поскольку по условию она ни одного из них не пересекает.