Математикадан республикалық олимпиада, 2011-2012 оқу жылы, 10 сынып

${{\omega }_{1}}$, ${{\omega }_{2}}$, ${{\omega }_{3}}$ — ауданы $S$-қа тең ${{A}_{1}}{{A}_{2}}{{A}_{3}}$ үшбұрышының сырттан іштей сызылған шең-берлері. ${{\omega }_{1}}$ шеңбері ${{A}_{2}}{{A}_{3}}$ қабырғасын ${{B}_{1}}$ нүктесінде (және ${{A}_{1}}{{A}_{2}}$ мен ${{A}_{1}}{{A}_{3}}$ қабырғала-рын) жанайды. ${{A}_{1}}{{B}_{1}}$ түзуі ${{\omega }_{1}}$ шеңберін ${{B}_{1}}$ және ${{C}_{1}}$ нүктелерінде қиып өтеді. ${{A}_{1}}{{A}_{2}}{{C}_{1}}{{A}_{3}}$ төртбұрышының ауданын ${{S}_{1}}$-деп белгілейік. Осыған ұқсас жолмен ${{S}_{2}}$ және ${{S}_{3}}$ сандарын анықтаймыз. $\dfrac{1}{S}\le \dfrac{1}{{{S}_{1}}}+\dfrac{1}{{{S}_{2}}}+\dfrac{1}{{{S}_{3}}}$ болатынын дәлелдеңдер. ( А. Васильев )

Комментарий/решение

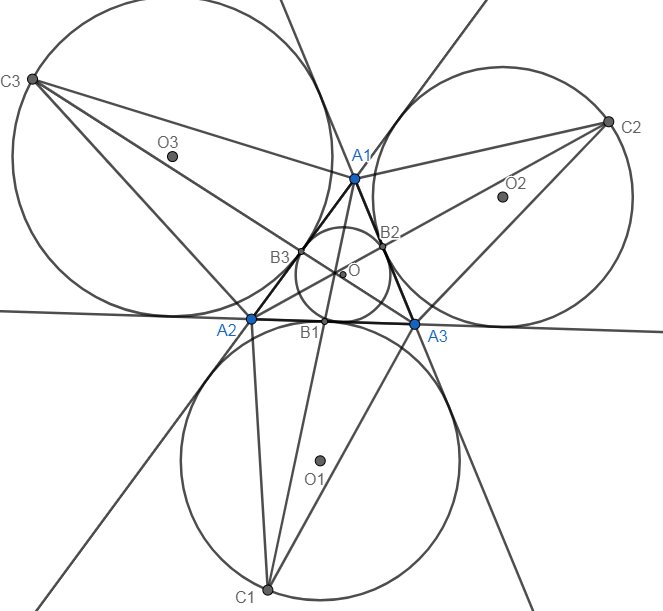
Обозначим правую часть неравенства как $X$, пусть $R_{1}$ радиус вневписанной окружности касающийся стороны $A_{2}A_{3}$ и $C_{1}T$ высота опущенная на сторону $A_{2}A_{3}$, так же $R$-радиус вписанной в $A_{1}A_{2}A_{3}$ и $R_{2},R_{3}$ радиусы вневписанных, тогда $ C_{1}T \leq 2R_{1}$ получаем $\dfrac{1}{R_{1}} = \dfrac{A_{2}A_{3}}{\dfrac{2R_{1} \cdot A_{2}A_{3}}{2}} \leq \dfrac{A_{2}A_{3}}{\frac{C_{1}T \cdot A_{2}A_{3}}{2}} = \dfrac{ A_{2}A_{3}}{S_{1}}$ или $\dfrac{1}{R_{1} \cdot A_{2}A_{3}} \leq \dfrac{1}{S_{1}}$ аналогично и с другими, суммируя получаем $Y=\dfrac{1}{R_{3} \cdot A_{1}A_{2}} + \dfrac{1}{R_{2} \cdot A_{1}A_{3}} + \dfrac{1}{R_{1} \cdot A_{2}A_{3}} \leq X$ докажем что $\dfrac{1}{S} \leq Y$ , так как $S=pR=\dfrac{A_{1}A_{2}+A_{2}A_{3}+A_{1}A_{3}}{2}R$ получаем

$\dfrac{1}{R_{1} \cdot A_{2}A_{3}} + \dfrac{1}{R_{2} \cdot A_{1}A_{3}} + \dfrac{1}{R_{3} \cdot A_{1}A_{2}} \geq \dfrac{2}{R \cdot (A_{1}A_{2}+A_{1}A_{3}+A_{2}A_{3})} $

По известному свойству $\dfrac{1}{R}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}$ подставляя получаем для первого слагаемого

$\dfrac{1}{R_{1} \cdot A_{2}A_{3}} \geq \dfrac{2}{R_{1}(A_{1}A_{2}+A_{2}A_{3}+A_{1}A_{3})}$

откуда $A_{1}A_{2}+A_{1}A_{3} \geq A_{2}A_{3}$ что верно по неравенству треугольников, аналогично и для двух других слагаемых, получаем что $\dfrac{1}{S} \leq Y \leq X$ или $\dfrac{1}{S} \leq X$