Областная олимпиада по информатике 2019 год
Задача A. Волшебство на матрицах
Ограничение по времени:
2 секунды
Ограничение по памяти:
256 мегабайт
Юный волшебник Асхат научился новому заклинанию - теперь он умеет заменять любую матрицу ее префиксной суммой!
Дабы закрепить новые знания, он решил немного попрактиковаться. Он раздобыл матрицу очень большого размера, каждый элемент которой равен $1$, и очень много раз применил к ней вышеописанное заклинание.
В этой задаче вам предстоит показать, что ваши навыки программирования ничем не уступуают магии. На каждый соответствующий запрос, а их будет очень много, найдите чему было равно число в $i$-м ряду в $j$-й строке матрицы после $k$ применений заклинания. Поскольку эти числа могут быть довольно большими, выведите остаток от их деления на 1000000007.
Формат входного файла
Первая строка содержит целое положительное число $Q \; (1 <= Q <= 10^5)$ — количество запросов к вашей программе.
Каждая из следующих $Q$ строк описывает очередной запрос и содержит три целых положительных числа — номер строки $i$, номер столбца $j$ и количество предварительных применений заклинания $k$ $(1 <= i, j, k <= 10^5)$ соответственно.
Формат выходного файла
Выведите $Q$ целых чисел, по одному в строке — значение в ячейке в $i$-м ряду в $j$-й строке матрицы после $k$ применений заклинания, взятое по модулю 1000000007.
Система оценки
Подзадача 1 (10 баллов) — $1 <= Q <= 10, 1 <= i, j, k <= 100$
Подзадача 2 (10 баллов) — $1 <= i, j, k <= 100$
Подзадача 3 (10 баллов) — $1 <= i, j, k <= 10^3$
Подзадача 4 (10 баллов) — $i = 1$ или $j = 1$
Подзадача 5 (10 баллов) — $k = 1$
Подзадача 6 (50 баллов) — без дополнительных ограничений
Примеры:
Вход 2 2 3 1 1 1 3Ответ
6 1Вход
3 4 5 7 3 3 3 2 1 10Ответ
39600 100 11
Замечание
Напомним, что матрица - это двумерный массив (иначе говоря, таблица) содержащий целочисленные значения. Один из возможных примеров матрицы 3x4 приведен ниже: \begin{center} \begin{tabular}{|c|c|c|c|} \hline 1 & 2 & 3 & 4\\ \hline 4 & 7 & 0 & -2\\ \hline 5 & 9 & 2 & 6\\ \hline \end{tabular} \end{center}
Префиксной суммой называется матрица, где каждый элемент заменен на сумму чисел в соответствующуем ему прямоугольнике с противоположной вершиной в $(1, 1)$. Более формально, определим префиксную сумму матрицы $A$ как матрицу $B$ такую, что для любых $i > 0, \; j > 0$ выполняется \[B_{i, j} = A_{i, j} + B_{i - 1, j} + B_{i, j - 1} - B_{i - 1, j - 1}\]
В то время как значения в ячейках $B$ с $i = 0$ или $j = 0$ равны нулю.
Например перфиксной суммой данной матрицы \begin{center} \begin{tabular}{|c|c|c|c|} \hline 1 & 2 & 0 & 1\\ \hline 4 & 1 & 5 & 9\\ \hline 3 & 2 & 6 & 1\\ \hline 0 & 7 & 2 & 4\\ \hline \end{tabular} \end{center}
Будет следующая матрица: \begin{center} \begin{tabular}{|c|c|c|c|} \hline 1 & 3 & 3 & 4\\ \hline 5 & 8 & 13 & 23\\ \hline 8 & 13 & 24 & 35\\ \hline 8 & 20 & 33 & 48\\ \hline \end{tabular} \end{center}
комментарий/решение(6)
Задача B. Machine Vision
Ограничение по времени:
2 секунды
Ограничение по памяти:
256 мегабайт
\includegraphics[width=0.25\textwidth,natwidth=360,natheight=300,height=100pt]{abbey_road.png} НурлашКО для своего нового стартапа потребовалось получать текст по фотографии. Так как он только на стадии прототипа, его друг предложил использовать готовое решение предоставляемое платформой Muugle Cloud Vision API. Однако, возникла небольшая проблема в работе с этой платформой. В ответ на отправленную фотографию возвращался не текст, а отдельные слова и их локации в виде прямоугольников. Помогите НурлашКО переупорядочить слова и получить осмысленный текст. Более формально. Вам будет дано $N$ прямоугольников со сторонами параллельными осям координат и слова соответствующие каждому из них. Прямоугольник $B$ является соседом $A$ тогда и только тогда когда площадь пересечения их проекций на ось ординат положительна и $B$ ближайший, слева или справа от $A$, среди всех таких. Строчкой называется максимальное по включению подмножество прямоугольников где от каждого прямоугольника можно добраться до любого другого, возможно переходя по соседям. Высота строчки определяется высотой самого высокого прямоугольника в ней. Выведите все строчки предварительно упорядочив их по высоте в порядке убывания. В самой строчке для каждого прямоугольника выведите соответствующую ему слово в порядке от самого левого к правому. Гарантируется что если $A$ является соседом $B$, то и $B$ является соседом $A$. Соседи для прямоугольника, если таковые есть, всегда определяются однозначно. Смотрите замечание к тестовому примеру для лучшего понимания.
Формат входного файла
Первая строка входного файла содержит единственное целое положительное число $N(1 <=q N <=q 2*10^5)$ — количество прямоугольников.
Каждая из следующих $N$ строке содержит строчку из маленьких латинских букв и цифр $s_i (1 <=q |s_i| <=q 100000)$ и четыре целых числа $xl_i$, $yb_i$, $xr_i$, $yt_i$ $(1 <=q xl_i, yb_i, xr_i, yt_i <=q 10^9)$ — слово соответствующее прямоугольнику, координаты левого нижнего и правого верхнего угла соответственно.
Гарантируется что сумма длин всех $s_i$ не превосходит $2*10^5$. Также гарантируется что никакие два прямоугольника не пересекаются и не вкладываются, но могут касаться.
Формат выходного файла
Выведите ответ на задачу в соответствии с форматом описанным в условии. Каждую строчку следует выводить в отдельной строке. Слова следует разделять единичным пробелом.
Система оценки
Данная задача содержит две подзадачи:
- $1 <=q N <=q 2000$. Оценивается в $30$ баллов.
- $1 <=q N <=q 200000$. Оценивается в $70$ баллов.
Пример:
Вход 7 1 9 1 10 3 New 5 3 11 5 Happy 1 2 4 4 2 4 0 5 2 9 10 0 11 2 Year 11 2 15 4 0 6 1 7 3Ответ
Happy New Year 2 0 1 9
Замечание
\includegraphics[width=0.5\textwidth,natwidth=610,natheight=450]{example2.png}
Обратите внимание, что прямоугольники с цифрами $2$ и $0$ не могут быть соседями для прямоугольника со словом $Happy$. В первом случае площадь проекций $Happy$ и $2$ на ординату равна нулю. Во втором случае хоть и площадь пересечения равна единице, но прямоугольник $New$ находится ближе, в тоже время имея положительную площадь пересечения и именно он будет соседом $Happy$.
Расстояние между двумя прямоугольниками $A$ и $B$ - это кратчайшее среди всех попарных расстояний от множества точек ограниченных прямоугольником $A$ до множества точек ограниченного прямоугольником $B$.
комментарий/решение(1) Проверить мое решение
Задача C. Хан и массив
Ограничение по времени:
2 секунды
Ограничение по памяти:
512 мегабайт
Хан на день рождения получил массив из $n$ элементов. И начал с ним играться. Он взял каждый элемент и записал $m$ раз. Также у Хана есть любимое простое число $P$. Ему стало интересно, сколько существует подпоследовательностей, которые в сумме делятся на $P$. Помогите Хану узнать сколько таких подпоследовательностей.
Формат входного файла
В первой строке даны три целых числа $n$, $m$, $P$ через пробел — размер массива Хана; количество раз, которое он записывает каждое число в массиве; и простое число соответственно $(1 <= n <= 10^5, 1 <= m <= 10^9, 1 <= P <= 10^3)$.
Во второй строке даны $n$ целых чисел $a_1, a_2, ..., a_n$ — полученный Ханом массив на его день рождения $(1 <= a_i <= 10^9)$.
Формат выходного файла
Выведите одно число — количество подпоследовательностей, которые в сумме делятся на $P$. Так как это число может быть большим, выведите его остаток от деления на $1000000007$.
Система оценки
Подзадача 1 (10 баллов) — $ n <= 10^5$, $m <= 10^5,$ $P = 2 $.
Подзадача 2 (10 баллов) — $ n * m <= 20$, $P <= 1000 $.
Подзадача 3 (10 баллов) — $ n * m * P <= 10^6, $.
Подзадача 4 (20 баллов) — $ n * m <= 250000$, $P <= 500 $.
Подзадача 5 (50 баллов) — $ n <= 10^5$, $m <= 10^9$, $P <= 1000 $.
Пример:
Вход 3 2 5 3 7 4Ответ
11
Замечание
Хан преобразует изначальный массив следующим образом. Пусть $a_1, a_2, ..., a_n$ будет изначальным массивом. И заведем пустой массив $b$. Один за одним, слева направо будем обрабатывать элементы массива $a$ и элемент $a_i$ припишем к $b$ ровно $m$ раз. Хан будет решать задачу над полученным массивом $b$.
Подпоследовательность — последовательность, которая получается путем удаления нескольких, возможно ноль, элементов изначальной последовательности.
В первом примере, массив $b$ будет выглядеть следующим образом: $3, 3, 7, 7, 4, 4$. Вот все $11$ подпоследовательности, сумма которых делится на $5$: $[3, 7]$, $[3, 7]$, $[3, 7]$, $[3, 7]$, $[3, 3, 4]$, $[3, 3, 4]$, $[3, 3, 7, 7]$, $[7, 4, 4]$, $[7, 4, 4], $[3, 7, 7, 4, 4], $[3, 7, 7, 4, 4]$.
комментарий/решение(2) Проверить мое решение
Задача D. Чередующие тренировки
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
Алан очень сильно любит решать задачи по программированию и играть шахматы. В обоих сферах он хочет преуспеть, стать легендарным гроссмейстером. Айдос как опытный тренер предложил ему у него потренироваться.
У Айдоса определенное расписание на каждый из следующих $n$ дней. В каждый из дней Айдос тренирует только один вид, либо программирование, либо шахматы. Алан хочет выбрать несколько подряд идущих дней для тренировки. Также Алан заметил, что если два дня подряд тренироваться в одной и той же сфере, то он устает, т.е. Алану надо чередовать шахматы и программирование. Помогите Алану выбрать максимальное количество подряд идущих дней так, чтобы он за этот период не устал тренироваться.
Формат входного файла
Первая строка входных данных содержит целое цисло $n$ ($1 <= n <= 2\cdot 10^5$) — количество тренировочных дней у Айдоса. Вторая строка содержит $n$ цифр $0$ или $1$ без пробелов — $i$-я цифра $0$ если в $i$-й день Айдос тренирует программирование, иначе Айдос тренирует шахматы.
Формат выходного файла
Выведите одно число — максимальное количество подряд идущих тренировочных дней для Алана.
Система оценки
В данной задаче 50 тестов, прохождение каждого теста оценивается в 2 балла:
Подзадача 1: 2 тестовых примера из условия
Подзадача 2: $n <= 3$. 13 тестов
Подзадача 3: $n <= 100$. 5 тестов
Подзадача 4: $n <= 5000$. 12 тестов
Подзадача 5: $n <= 200000$. 18 тестов
Примеры:
Вход 4 0 1010Ответ
4Вход
5 3 01011 1 3 2 5 4 5Ответ
3
Замечание
В первом тесте Алан может все дни тренироваться.
Во втором тесте Алан может тренироваться со 2-го по 4-й день: во 2-й день программирование, в 3-й день шахматы и в 4-й день программирование. Заметим, что первый, второй день Алан не может тренироваться, так как в эти дни только программирование и Алан сильно устанет.
комментарий/решение(5) Проверить мое решение
Задача E. Меж двух миров
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
Алан живет в мире под номером $A$. Нурдаулет живет в мире под номером $B$. В мире $A$, если одна строка является префиксом другой, то они считаются одинаковыми. У Нурдаулета есть $n$ строк, он хочет узнать количество неупорядоченных пар $i, j$ таких, что Алану они покажется одинаковыми. Помогите Нурдаулету с задачей. Обозначим $|s|$ как длину строки $s$. Строка $s$ является префиксом строки $t$, если $|s| <= |t|$ и строка $s$ равна строке, образованной из первых $|s|$ символов строки $t$.
Формат входного файла
В первой строке дается единственное число $n (1 <= n <= 100000)$ — количество строк.
В следующих $n$ строках дается по одной строке $s_i$. Гарантируется, что суммарная длина строк не превышает $500000$.
Формат выходного файла
Выведите единственное число — ответ на задачу.
Система оценки
В 40 процентах тестов $n <= 100$.
В 20 процентах тестов, длины всех строк равны.
Пример:
Вход 3 ab abc abОтвет
3
комментарий/решение(7) Проверить мое решение
Задача F. Yosik - город где сбываются мечты
Ограничение по времени:
1 секунда
Ограничение по памяти:
256 мегабайт
Yosik - это город Казахстана где сбываются мечты миллионов. И при этом Yosik - важнейший экономический центр всего мира. Yosik, наряду с Лондоном и Токио, называют одним из трёх основных центров мировой экономики. Ну конечно же, без мэра CMaster город не был бы таким популярным. Он приложил все свои усилия чтобы достичь этого. Но экономическая война между другими странами повлиял негативно на экономику Yosik-a. Мэр хочет улучшить качество некоторых дорог в городе. И в городе существует $n$ районов. Каждый район имеет экономический статус: Высокий или Низкий. И чтобы мэр CMaster принял правильное решение об улучшении дорог во время кризиса в городе он должен узнать сколько пар Высоких важности районов это дорога соединяет. То есть, дорога соединяет два Высоких важности районов $(a, b)$ если и только если все пути между этими двумя районами проходят через эту дорогу. И есть $q$ событии двух видов: 1) Сделать статус района $v$ $(1 <=q v <=q n)$ Высоким если он Низкий, а иначе сделать его Низким. 2) Для дороги $i$ сказать количество пар районов $(a, b)$ с Высоким статусом что дорога $(1 <=q i <=q m)$ лежит на всех путях между этими районами $(a, b)$. И при этом пары $(a, b)$ и $(b, a)$ считаются одинаковыми Город можно представить как связный неориентированный граф с $n$ вершинами и $m$ ребрами. Где вершина это район а ребро это дорога. Каждый район имеет статус экономического важности либо Высокий либо Низкий. Вначале все районы имеют Низкий важность для экономики. Из района может существовать дорога которая соединяет район с собой (петля), но не существует кратные ребра, то есть дороги которые соединяют одинаковую пар вершин.
Формат входного файла
На первой строке даны 3 числа $n$, $m$ и $q$, количество районов, дорог и событии, соответственно.
Далее следует $m$ чисел - неориентированные ребра в Yosik-e.
В графе не существует две одинаковых ребер, но могут быть петли
Потом вам дается запросы в виде $(type, number)$. Если $type = 1$, то это первый тип запросов и $number$ означает номер вершины, $(1 <=q number <=q n)$. А если $type = 2$, то это второй тип запросов и число означает номер ребра в порядке входных данных, $(1 <=q number <=q m)$
Формат выходного файла
Для каждого запроса вида 2, вы должны вывести количество пар город $(a, b)$ которые имеют статус Высокой важности что ребро $i$ лежит на всех путях между этими вершинами $(a, b)$
Система оценки
Данная задача содержит четыре подзадач:
1. $1 <=q n, q <=q 10$. Подзадача оценивается в 10 баллов
2. $1 <=q n, m, q <=q 300$. Подзадача оценивается в 14 баллов
3. $1 <=q n, m, q <=q 2000$. Подзадача оценивается в 22 баллов
4. Город является деревом $1 <=q n, q <=q 10^5, m = n - 1$. Подзадача оценивается в 24 баллов
5. $1 <=q n, m, q <=q 10^5$. Подзадача оценивается в 30 баллов
Пример:
Вход 9 10 10 1 2 3 2 4 3 2 4 3 5 8 5 9 8 5 6 5 7 7 6 1 2 1 1 1 4 2 5 2 1 1 9 1 7 1 5 2 5 2 2Ответ
0 2 9 0
Замечание
Граф из первого теста (перед запросом с номером 5)
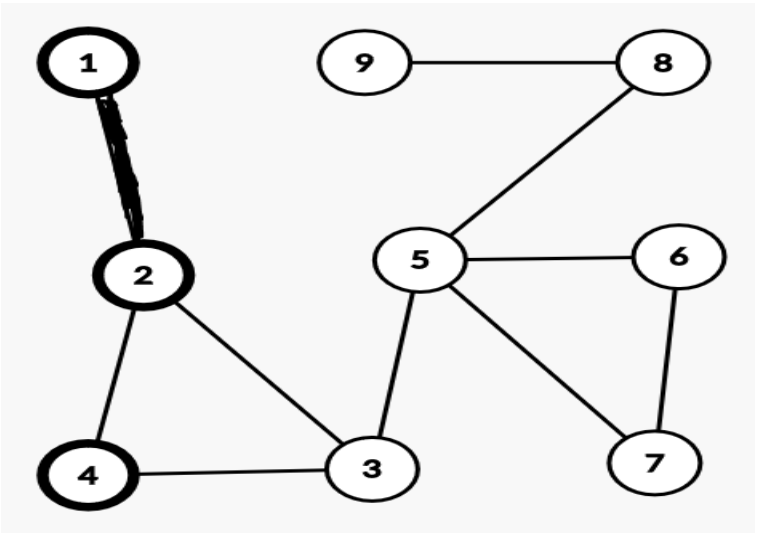
комментарий/решение(6) Проверить мое решение