4-я международная Иранская олимпиада по геометрии, 2017 год, первая лига, 7-8 классы
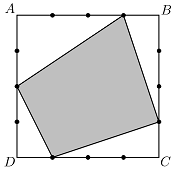
Задача №1. Каждая сторона квадрата $ABCD$ со стороной 4 поделена на равные части тремя точками (см. рис. ниже). На каждой стороне выбрано по одной из этих точек. Выбранные точки последовательно соединены таким образом, что получился четырёхугольник. Чему может быть равна площадь этого четырёхугольника? Выпишите все возможные значения площади, обосновывать ответ не требуется.
комментарий/решение(2)
комментарий/решение(2)
Задача №3. В правильном пятиугольнике $ABCDE$ прямая, проходящая через точку $C$ перпендикулярно $CD$, пересекает отрезок $AB$ в точке $F$. Докажите, что $AE+AF=BE$.
комментарий/решение(1)
комментарий/решение(1)
Задача №4. На плоскости расположены точки $P_1$, $P_2, \ldots, P_{100}$, никакие три из которых не лежат на одной прямой. Для любой тройки точек $P_i$, $P_j$, $P_k$ $(i < j < k)$ назовем образованный ими треугольник правильно ориентированным, если обход из точки $P_i$ по отрезкам $P_iP_j$, $P_jP_k$, $P_kP_i$ происходит в направлении по часовой стрелке. Может ли количество правильно ориентированных треугольников быть равно в точности 2017?
комментарий/решение
комментарий/решение
Задача №5. Дан равнобедренный треугольник $ABC$ ($AB=AC$). Пусть $l$ — прямая, проходящая через точку $A$ параллельно $BC$, $D$ — произвольная точка на прямой $l$. Обозначим через $E$ и $F$ основания перпендикуляров, опущенных из точки $A$ на $BD$ и $CD$ соответственно. Пусть $P$ и $Q$ — проекции точек $E$ и $F$ на прямую $l$. Докажите, что $AP+AQ \leqslant AB$.
комментарий/решение(1)
комментарий/решение(1)