Олимпиада Туймаада по математике. Младшая лига. 2007 год
Задача №1. Даны два натуральных числа $a < b$. Докажите, что из любых $b$
последовательных натуральных чисел можно выбрать два числа, произведение
которых делится на $ab$.
(
С. Берлов
)
комментарий/решение(4)
комментарий/решение(4)
Задача №2. Несовпадающие квадратные трехчлены $f(x)$ и $g(x)$ отличаются друг от
друга перестановкой коэффициентов. Может ли оказаться, что $f(x)\geq g(x)$
при всех вещественных $x$?
(
А. Голованов
)
комментарий/решение(1)
комментарий/решение(1)
Задача №3. Квадрат $600\times 600$ разбит на фигурки из 4 клеток вида
комментарий/решение
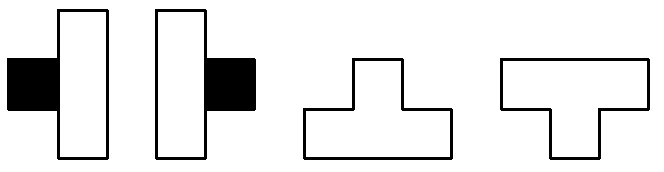
комментарий/решение
Задача №4. Дан остроугольный неравнобедренный треугольник $ABC$.
Точка $H$ — его ортоцентр, точки $O$ и $I$ — центры его описанной
и вписанной окружностей соответственно.
Описанная окружность треугольника $OIH$ проходит через вершину~$A$.
Докажите, что один из углов треугольника равен $60^\circ$.
(
из материалов олимпиад
)
комментарий/решение(1)
комментарий/решение(1)
Задача №5. В какое наименьшее количество цветов можно покрасить
все натуральные числа так, чтобы
любые два натуральных числа,
отличающиеся в 4 или 8 раз, были покрашены в разные цвета?
(
А. Голованов
)
комментарий/решение
комментарий/решение
Задача №6. В однокруговом шахматном турнире участвуют по $10$ игроков из двух
стран. За победу дается одно очко, за ничью — пол-очка, за поражение —
ноль. Все игроки набрали разное число очков. Докажите, что один из шахматистов
набрал во встречах со своими соотечественниками не меньше очков,
чем во встречах с игроками из другой страны.
(
из материалов олимпиад
)
комментарий/решение
комментарий/решение
Задача №7. На стороне $AB$ треугольника $ABC$ выбраны точки $X$ и $Y$, на
стороне $AC$ — точка $Z$, и на стороне $BC$ — точка $T$. При этом
$XZ \parallel BC$, $YT \parallel AC$. Прямая $TZ$ пересекает описанную
окружность треугольника $ABC$ в точках $D$ и $E$. Докажите, что точки
$X$, $Y$, $D$ и $E$ лежат на одной окружности.
(
из материалов олимпиад
)
комментарий/решение
комментарий/решение
Задача №8. На бесконечной клетчатой плоскости стоит несколько шахматных коней.
При этом никакая клетка не находится под боем более, чем одного коня.
(В частности, клетка, на которой стоит конь, может биться другим конем, но
не двумя сразу). Саша обвел контур прямоугольника $14\times 16$. Какое
наибольшее количество коней могло попасть в этот прямоугольник?
(
С. Берлов
)
комментарий/решение
комментарий/решение