Олимпиада Туймаада по математике. Старшая лига. 2005 год
Задача №1. В клетках таблицы $11 \times 11$ расставлены все натуральные числа от
1 до 121. Дима посчитал произведение чисел в каждой строке, а Саша —
произведение чисел в каждом столбце. Могли ли они получить одинаковые наборы
из 11 чисел?
(
С. Берлов
)
комментарий/решение
комментарий/решение
Задача №2. Шесть членов команды Фаталии на Международной математической олимпиаде
отбираются из 13 кандидатов. На отборочной олимпиаде кандидаты набрали
$a_1$, $a_2$, $\dots$, $a_{13}$ баллов ($a_i\ne a_j$ при $i\ne j$).
Руководитель команды заранее выбрал 6
кандидатов и теперь хочет, чтобы в команду попали именно они. С этой целью он
подбирает многочлен $P(x)$ и вычисляет творческий потенциал
каждого кандидата по формуле $c_i=P(a_i)$. При каком минимальном $n$ он
заведомо сможет подобрать такой многочлен $P(x)$ степени не выше $n$, что
творческий потенциал любого из его шести кандидатов окажется строго
больше, чем у каждого из семи оставшихся?
(
Ф. Петров,
К. Сухов
)
комментарий/решение
комментарий/решение
Задача №3. Организаторы математического конгресса
обнаружили, что, если любого из участников поселить в одноместный номер,
то всех остальных можно будет расселить по двухместным номерам,
в каждом из которых обитатели будут знакомы друг с другом.
Докажите, что любой участник может организовать круглый стол по теории графов, в котором, кроме него, будет участвовать еще четное число людей, и каждый участник будет знаком с обоими своими соседями по столу. ( С. Берлов, С. Иванов )
комментарий/решение
Докажите, что любой участник может организовать круглый стол по теории графов, в котором, кроме него, будет участвовать еще четное число людей, и каждый участник будет знаком с обоими своими соседями по столу. ( С. Берлов, С. Иванов )
комментарий/решение
Задача №4. Дан треугольник $ABC$. Точки $A_1$, $B_1$ и $C_1$ — точки касания
вневписанных окружностей треугольника со сторонами $BC$, $CA$ и $AB$
соответственно. Докажите, что из отрезков $AA_1$, $BB_1$ и $CC_1$
можно составить треугольник.
(
Л. Емельянов
)
комментарий/решение(1)
комментарий/решение(1)
Задача №5. В клетках доски, изображенной на рисунке, стоят несколько ладей,
которые бьют все клетки (считается, что ладья бьет клетку, на которой стоит).
Докажите, что можно убрать несколько ладей, оставив не более 11, так,
чтобы оставшиеся ладьи по-прежнему били все клетки.
комментарий/решение
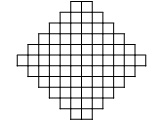
комментарий/решение
Задача №6. Даны натуральное число $n$ и бесконечная последовательность правильных
дробей $x_0={a_0\over n}$, $x_1={a_1\over n+1}$,
$x_2={a_2\over n+2}$, $\dots$ ($a_i < n+i$).
Докажите, что существуют такое натуральное число $k$ и такие целые числа
$c_1$, $c_2$, $\dots$, $c_k$, что $c_1x_1+c_2x_2+\dots+c_kx_k=1.$
(
М. Дубашинский
)
комментарий/решение
комментарий/решение
Задача №7. Точка $I$ — центр вписанной окружности треугольника $ABC$.
Окружность, проходящая через вершины $B$ и $C$,
пересекает отрезки $BI$ и $CI$ в точках $P$ и $Q$ соответственно.
Известно, что $BP\cdot CQ=PI\cdot QI$. Докажите, что описанная окружность
треугольника $PQI$ касается описанной окружности исходного треугольника.
(
С. Берлов
)
комментарий/решение
комментарий/решение
Задача №8. Для любых положительных чисел $a$, $b$ и $c$, удовлетворяющих условию
$a^2+b^2+c^2=1$, докажите неравенство
$${a\over a^3+bc} + {b\over b^3+ca} + {c\over c^3+ab} > 3 .$$
(
А. Храбров
)
комментарий/решение(5)
комментарий/решение(5)