Олимпиада имени Леонарда Эйлера
2014-2015 учебный год, II тур регионального этапа

Задача №1.  На столе лежит палочка длиной 10 см. Петя ломает её на две части и кладёт обе получившиеся палочки на стол. С одной из лежащих на столе палочек Вася проделывает ту же операцию, потом то же делает Петя и т.д., по очереди. Петя хочет, чтобы после 18 разломов все получившиеся палочки были короче 1 см. Вася хочет помешать Пете. Кто из них имеет возможность добиться своей цели независимо от действий соперника? ( И. Рубанов, С. Берлов )
комментарий/решение(1)

---

Задача №2.  Зрители оценивают фильм целым числом баллов от 0 до 10. В каждый момент времени рейтинг фильма вычисляется как сумма всех выставленных оценок, делённая на их количество. В некоторый момент времени $T$ рейтинг был целым числом, а затем с каждым новым проголосовавшим зрителем уменьшался на единицу. Какое наибольшее количество зрителей могло проголосовать после момента $T$? ( Р. Женодаров, О. Дмитриев )
комментарий/решение(1)

---

Задача №3.  В трапеции $ABCD$, где $AD \parallel BC$, угол $B$ равен сумме углов $A$ и $D$. На продолжении отрезка $CD$ за вершину $D$ отложен отрезок $DK = BC$. Докажите, что $AK = BK$. ( Б. Обухов )
комментарий/решение(1)

---

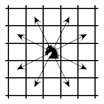
Задача №4. На шахматной доске размером $20\times20$ расставлены 220 коней, которые бьют все свободные клетки. Докажите, что можно убрать 20 коней таким образом, чтобы оставшиеся кони били все свободные клетки. Напомним, что конь бьёт буквой «Г» (см. рисунок).

( С. Берлов )
комментарий/решение(1)

---