Городская Жаутыковская олимпиада по математике, 8 класс, 2022 год
Задача №1. В выпуклом четырёхугольнике $ABCD$ точки $M$, $N$, $P$ и $Q$ являются серединами сторон $AB$, $BC$, $CD$ и $DA$ соответственно. Известно, что $MP=NQ$. Докажите, что диагонали $AC$ и $BD$ перпендикулярны.
комментарий/решение
комментарий/решение
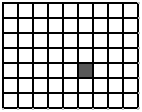
Задача №2. Дана сетчатая таблица $9\times 7$, в которой одна клетка закрашена (см. рис.). Сколько прямоугольников, стороны которого идут по линиям сетки, содержат эту закрашенную клетку?
комментарий/решение
комментарий/решение
Задача №3. Пусть $x$, $y$, $z$ — положительные числа. Докажите неравенство: $$x^2+xy^2+xyz^2 \ge 4xyz-4.$$
комментарий/решение(2)
комментарий/решение(2)
Задача №4. Набор чисел $a_1$, $a_2$, $\ldots$, $a_n$ является перестановкой чисел 1, 2, $\ldots$, $n$ в каком-то порядке. Для какого натурального $n$ возможно такое, что числа $$0, \ a_1,\ a_1 + a_2, \ \ldots, \ a_1 +a_2+ a_3+\ldots +a_n$$ дают попарно различные остатки при делении на $n+1$?
комментарий/решение
комментарий/решение
Задача №5. В выпуклом четырехугольнике $PQRS$ даны длины сторон: $PQ=40$, $PS=60$ и $RS=20$. Найдите значение $\angle QRS$, если $\angle QPS=\angle RSP=60{}^\circ$.
комментарий/решение(1)
комментарий/решение(1)
Задача №6. «Набором различных простых делителей» натурального числа назовём все его простые делители, перечисленные без повторений. Например, у числа 40 «набор различных простых делителей» — это 2 и 5. Даны два числа $A=2^k-2$ и $B=2^k \cdot A$, где $k \ge 2$. Докажите, что числа $A+1$ и $B+1$ имеют один и тот же «набор различных простых делителей».
комментарий/решение(1)
комментарий/решение(1)
Задача №7. Найдите все тройки действительных чисел $(x, y, z)$, удовлетворяющих системе уравнений: \[\left\{ \begin{array}{l} xy = z - x - y,\\ xz = y - x - z,\\ yz = x - y - z. \end{array} \right.\]
комментарий/решение(1)
комментарий/решение(1)
Задача №8. Дано множество $M=\{1, 2, \ldots, 9\}$. Пусть $S$ — подмножество $M$ такое, что суммы во всех парах чисел из $S$ различны. Например, в подмножестве $\{1, 2, 3, 5\}$ нет пары чисел с одинаковой суммой и такое подходит, а в подмножестве $\{1,2,3,4,5\}$ найдутся две пары с одинаковой суммой $(1+4=2+3)$ и такое не подходит. Какое наибольшее количество элементов может быть в $S$? Напоминаем, что в любом множестве не должно быть одинаковых чисел.
комментарий/решение
комментарий/решение