Математикадан республикалық олимпиада, 2009-2010 оқу жылы, 11 сынып

Теріс емес $x, y$ сандары үшін теңсіздікті дәлелдеңдер: $$\sqrt{x^2 - x + 1}\sqrt{y^2 - y + 1} + \sqrt{x^2 + x + 1}\sqrt{y^2 + y + 1} \ge 2(x + y).$$ ( М. Кунгожин )

Комментарий/решение

Дадим данному неравенству геометрическую интерпретацию.

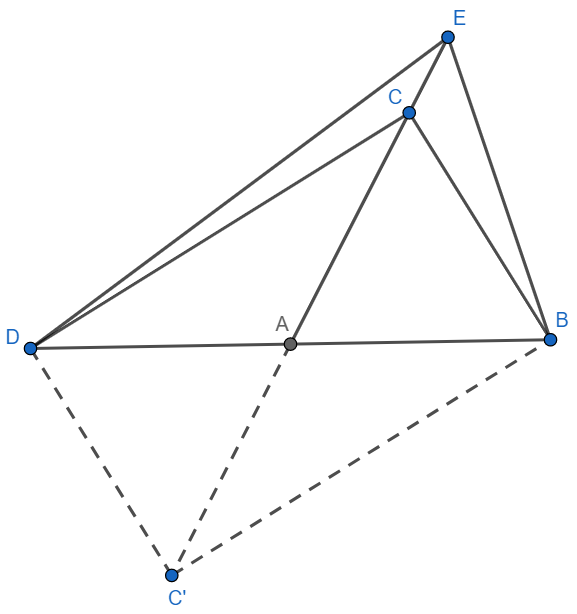
Пусть на плоскости имеется отрезок $BD=2$, точка $A$ середина $BD$ , пусть на этой же плоскости точка $C$ такая что $\angle BAC = 60^{\circ}$ и $AC=x$, так же пусть $E$ лежит на прямой $AC$ и такая что $AE=y$, тогда по теореме косинусов получаем $CB=\sqrt{x^2-x+1} , \ CD=\sqrt{x^2+x+1} , \ BE=\sqrt{y^2-y+1} , \ DE=\sqrt{y^2+y+1}$

Отразим симметрично точку $C$ относительно $A$ до параллелограмма $BDCC'$, тогда

$C'D=CB, \ CD= C'B$ применяя неравенство Птолемея для четырехугольника $C'DBE$ получаем $C'D \cdot BE + C'B \cdot DE \geq C'E \cdot BD $ или

$\sqrt{x^2-x+1} \sqrt{y^2-y+1} + \sqrt{x^2+x+1} \cdot \sqrt{y^2+y+1} \geq 2(x+y) $

$$ \sqrt{x^2-x+1}\sqrt{y^2-y+1}+\sqrt{x^2+x+1}\sqrt{y^2+y+1}\geq 2(x+y)$$

$$ x^4+x^2+1=(x^2-x+1)(x^2+x+1)\Rightarrow x^2-x+1=\frac{ x^4+x^2+1}{x^2+x+1}\Rightarrow$$

$$\Rightarrow \frac{\sqrt{x^4+x^2+1}\sqrt{y^4+y^2+1}}{\sqrt{x^2+x+1}\sqrt{y^2+y+1}}+\sqrt{x^2+x+1}\sqrt{y^2+y+1}\geq 2(x+y)$$

$$ \frac{\sqrt{x^4+x^2+1}\sqrt{y^4+y^2+1}}{\sqrt{x^2+x+1}\sqrt{y^2+y+1}}+\sqrt{x^2+x+1}\sqrt{y^2+y+1}\geq 2 \sqrt{x^4+x^2+1}\sqrt{y^4+y^2+1}$$

$$ \sqrt{x^4+x^2+1}\sqrt{y^4+y^2+1}\geq (x+y)\Rightarrow$$

$$ \sqrt{x^4+x^2+1}\sqrt{y^4+y^2+1}\geq \sqrt{x^2+1}\sqrt{y^2+1}\geq (x+y)\Rightarrow$$

$$\Rightarrow (x^2+1)(y^2+1)\geq (x+y)^2\Rightarrow$$

$$\Rightarrow (xy-1)^2\geq 0$$

Равенство достигается когда $x=\frac{1}{y}$

4-ші қатарда қате бар.

Есеп өте әдемі. Бірақ қатысушылардың барлығы шығарыпты. Геометриялық шешім барлығының ойына келе бермейді. Барлығы теңсіздіктің екі жағын квадраттау арқылы шығарған сыңайлы.

Пусть левая часть равно $A$, тогда по Коши Шварц:

$$4A=\sqrt{((2x-1)^2+3)((2-y)^2+3y^2)}+\sqrt{((2x+1)^2+3)((2+y)^2+3y^2)} \ge (2x-1)(2-y)+3y+(2x+1)(2+y)+3y=8(x+y)$$

Екі жағын квадраттап, ықшамдап, 2-ге қысқартқаннан кейін теңсіздік мына түрге келеді:

$(xy-1)^2+\sqrt{(x^4+x^2+1)(1+y^2+y^4)}\ge x^2+xy+y^2 $

$(xy-1)^2\ge 0$ және Коши-Буняковский теңсіздігінен:

$\sqrt{(x^4+x^2+1)(1+y^2+y^4)} \ge x^2+xy+y^2$

Done!

http://licpnz.ru/news/2021-12-11