Республиканская олимпиада по математике, 2009 год, 11 класс

Четырехугольник $ABCD$ вписан в окружность с центром $O$. Пусть прямые $AD$ и $BC$ пересекаются в точке $M$, прямые $AB$ и $CD$ — в точке $N$, прямые $AC$ и $BD$ — в точке $P$, а прямые $OP$ и $MN$ — в точке $K$. Докажите, что $\angle PKC=\angle AKP$.

Комментарий/решение

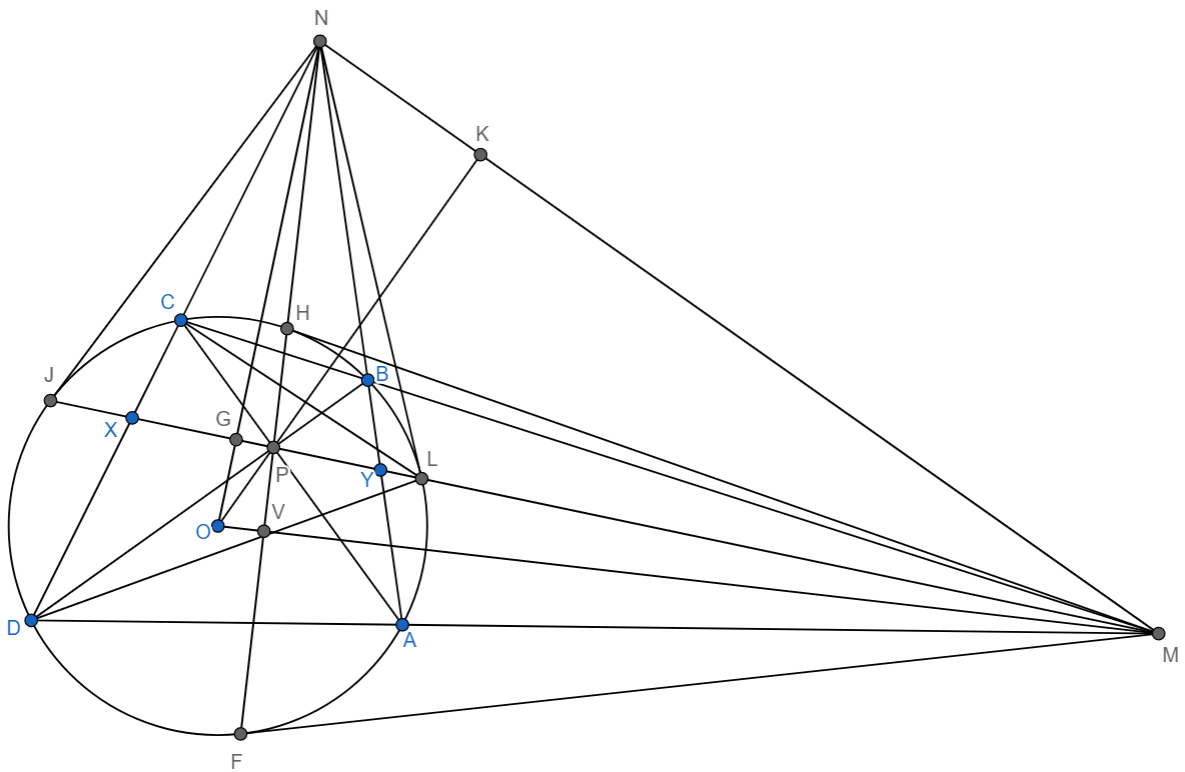
Докажем два утверждения, а именно:

1)Если провести касательные из вершины $N$ равные $NJ, \ NL$ то точки $J,P,L$ лежат на одной прямой.

Доказательство: Рассмотрим треугольник $CLD$ если в ней три хорды $BD, AC, JL$ пересекаются в точке $P$, то по теореме Чевы (в угловой форме) получаем:

$$\dfrac{\sin \angle DLJ}{\sin \angle CLJ}=\dfrac{DJ}{JC} , \ \ \dfrac{\sin \angle CDB}{\sin \angle BDL}=\dfrac{BC}{BL}, \ \ \dfrac{\sin \angle LCA}{\sin \angle ACD}=\dfrac{AL}{AD}$$

То есть $\dfrac{DJ}{JC} \cdot \dfrac{AL}{BL} \cdot \dfrac{BC}{AD}=1$ но так как $NJ=NL$ касательные, то из подобных треугольников $DJN,JCN$ и $NBC, NDA$ и $NBL,NAL$ соответственно получаем:

$$\dfrac{DJ}{JC}=\dfrac{JN}{CN}; \ \ \dfrac{BC}{AD} = \dfrac{BN}{DN}; \ \ \dfrac{AL}{BL} = \dfrac{NL}{BN}=\dfrac{JN}{BN}$$

Перемножая получаем $ JN^2=CN \cdot DN$ что верно, по теореме между касательной и секущей.

2) Докажем что и точка $M$ лежит на той же прямой что и точки $J,P,L$.

Доказательство: Пусть отрезок $JL$ пересекает прямые $ND,NO,NA$ соответственно в точках $X,G,Y$ тогда точка $G$ сопряженная относительно данной окружности точке $N$ так как $OG \cdot ON=R^2$ ($R$-радиус окружности) , тогда $JL$ поляра точки $N$, значит любая секущая проходящая через точку $N$ будет образовывать гармоническую четверку, в данном случае $(CD,NX)=1$ или $\dfrac{DX}{CX}=\dfrac{DN}{CN}(1)$ .

Если $M \in JL$ то по теореме Менелая для треугольника $DCA$ получаем:

$$\dfrac{DX}{CX} \cdot \dfrac{CP}{AP} \cdot \dfrac{AM}{MD } = 1 $$

Для треугольника $CMD$ и секущей $NA$ получаем :

$$\dfrac{AD}{AM} \cdot \dfrac{BM}{BC} \cdot \dfrac{CN}{DN} = 1$$

Учитывая $(1)$ получаем $\dfrac{AD}{BC} \cdot \dfrac{AB}{CD} \cdot \dfrac{CP}{AP}=1$ осталось доказать что оно верно, оно эквивалентно $\dfrac{AD}{BC}=\dfrac{AP}{PB}$ которая верна, получаем $M \in JL$ .

3) По свойству двойственности поляр получаем, что точка $N$ лежит на поляре точки $M$. Пусть $MF,MH$ касательные и $V \in FH \cap MO$ , тогда $V$ сопряженная точка $M$ относительно окружности , так как $OV \cdot OM=R^2$ , рассмотрим некую точку $P'$ такую что $OP \cdot OP'=R^2$ тогда треугольники $OGP$ и $ONP'$ подобны, откуда $\angle NP'A=90^{\circ}$ аналогично треугольники $OPV$ и $OP'M$ подобны, откуда $\angle OP'M=90^{\circ}$ значит точка $P'=K$ или $OK \perp MN$.

4) Заметим что точки $O,H,K,M,F$ лежат на одной окружности с диаметром $OM$ , тогда по свойству секущих получаем $NK \cdot MN = NH \cdot NF = NC \cdot ND$ значит четырехугольник $DCKM$ вписанный, так же как и $DNKA$ откуда $\angle ADC=\angle NKC = \angle AKM$ или $\angle PKC = 90^{\circ}-\angle NKC = \angle 90^{\circ}-AKM = \angle AKP$ .