Районная олимпиада, 2012-2013 учебный год, 10 класс
Комментарий/решение:
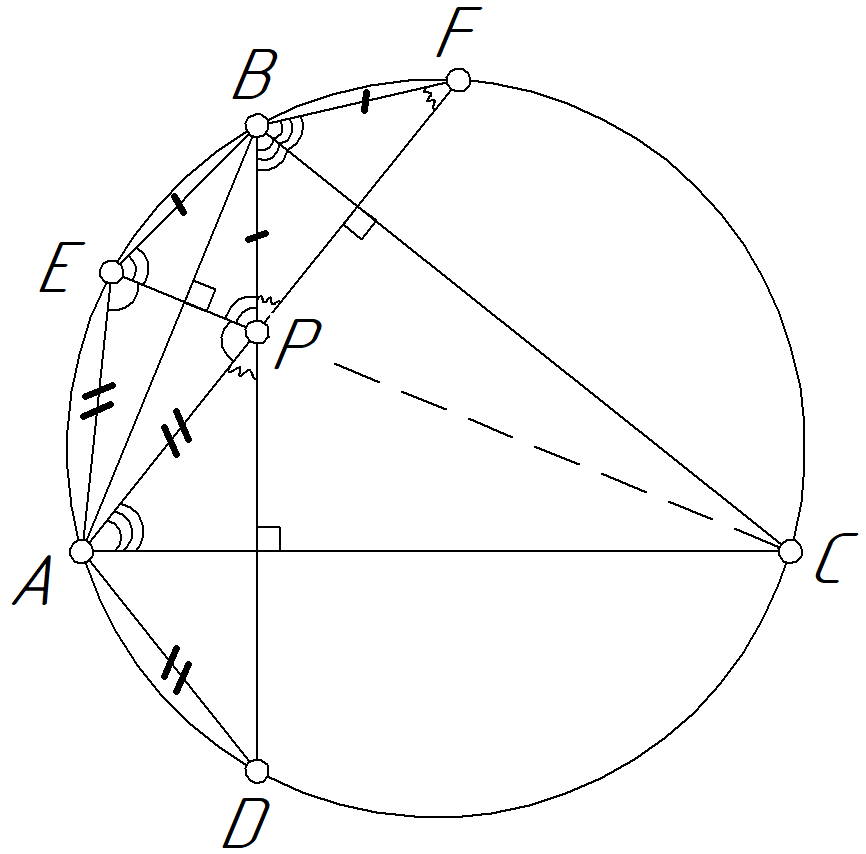
1) Из условия следует, что $E$ и $P$ симметричны относительно $AB$;
$D$ и $P$ симметричны относительно $AC$;
$F$ и $P$ симметричны относительно $BC$;
Отсюда следует, что $\triangle BEP,\triangle AEP,\triangle APD,\triangle BPF-$ равнобедренные
2)Из $[1]$ следует, что $\angle BEP=\angle BPE;\angle AEP=\angle APE;\angle BPF=\angle BFP$
3) Если доказать, что $\angle APF=180^{\circ}$, можно утверждать, что точка $P$ лежит хотя бы на одной из высот (а именно $AF$)
4)Рассмотрим сумму углов, из которых состоит $\angle APF$
$\angle APF= \angle APE+ \angle EPB+ \angle BPF$
Из $[2]$ следует, что $\angle APF= \angle AEP+ \angle BEP+ \angle BFP$
Обратим внимание, что $AEBF$ вписан в окружность. Свойство вписанных в окружность четырёхугольников-сумма противоположных углов равна $180^{\circ}$
$\angle APF= \angle AEP+ \angle BEP+ \angle BFP= \angle AEB+ \angle BFP=180^{\circ}$
5) Теорема: все высоты треугольника пересекаются в одной точке
6) Из $[5]$ следует, что достаточно доказать, что $P$ лежит и на второй высоте, чтобы $P$ стало точкой пересечения высот (это и просят доказать в задаче)
Аналогично $[3]$, покажем, что $\angle BPD=180^{\circ}$
Рассмотрим сумму углов, из которых состоит $\angle BPD$
$\angle BPD= \angle DPA+ \angle EPB+ \angle APE$
Сравнимся с выражением $[4]$
$\angle APF= \angle APE+ \angle EPB+ \angle BPF$
Покажем, что $ \angle BPF=\angle DPA$. Они равны как опирающиеся на равные дуги $AD$ и $AE$
Правые части выражений равны, значит и левые равны
$\angle BPD=\angle APF=180^{\circ}$
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.