Областная олимпиада по математике, 2006 год, 10 класс

Окружность, вписанная в треугольник $ABC$, касается сторон $AB$ и $BC$ в точках $E$ и $F$ соответственно. Точки $M$ и $N$ — основания перпендикуляров, опущенных из точек $A$ и $C$ на прямую $EF$. Докажите, что если стороны треугольника $ABC$ образуют арифметическую прогрессию и $AC$ — средняя сторона, то $ME+ FN = EF$.

Комментарий/решение

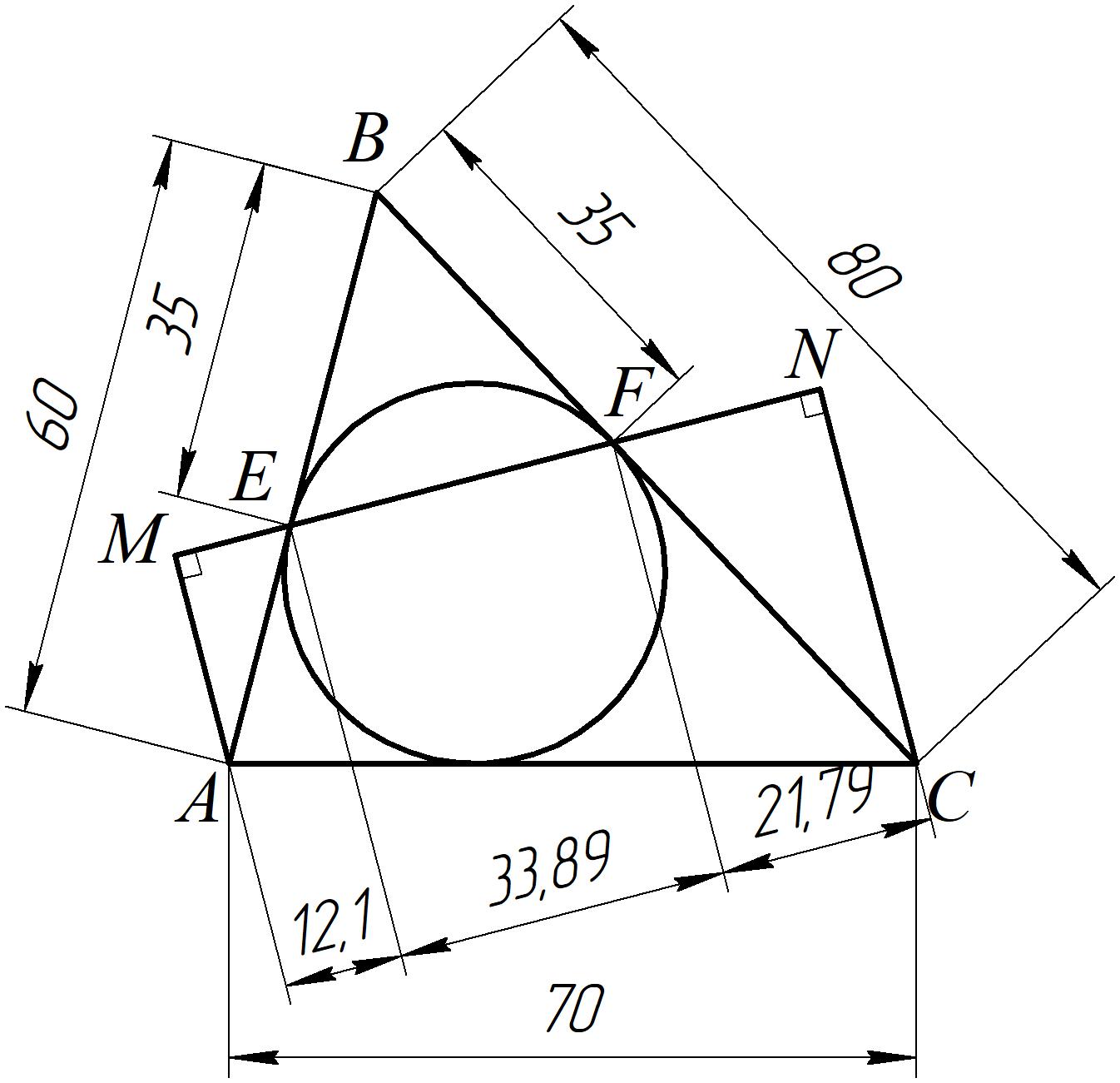
По условию $AC=\dfrac{AB+BC}{2}$. Пусть $O$ центр окружности вписанной в треугольник ABC. $OE \bot AB$ как касательная к окружности, $OF\bot BC$ по той же причине, $EB=BF$ как отрезки касательных исходящих из одной точки. Треугольник $EBF$ равнобедренный. Углы $MEA,BEF,BFE,NFC$ равны, Проведем $BH\bot EF$. Получим $MEA\sim HEB, BHF\sim CNF$.

Из точки $O$ опустим перпендикуляр на $OX$ на $AC$. $AO$ и $CO$ биссектрисы углов $A$ и $C$ соответственно. Получаем что треугольники $AOE$ и $AOX$ равны и равны треугольники $COF$ и $COX.$ Получили $AE=AX,$ $CX=CF,$ $AE+CF=AC.$

Вспомним,что $AC=\dfrac{AB+BC}{2}=\dfrac{AE+EB+BF+CF}{2}=\dfrac{AC}{2}+\dfrac{BE+BF}{2}$ или $BE=\dfrac{AC}{2}$. Вспомним подобия и получим $\dfrac{AE}{EB}=\dfrac{ME}{EH}$ и $\dfrac{CF}{BF}=\dfrac{FN}{FH}$ Пусть $AE=a,$ $CF=b,$ тогда $AC=a+b,$ тогда $\dfrac{a}{a+b}=\dfrac{ME}{EF}$ и $\dfrac{b}{a+b}=\dfrac{FN}{EF}$. Сложив их получим $\dfrac{ME+FN}{EF}=1$, что и требовалось доказать.

А в треугольнике EBF разве не EB=BF?

Решал давно, так не скажу. Вечером проверю, отпишусь

Ваша правда, в моем решении опечатка. Лень было проверять, в Компасе чирканул чертеж, оттуда все понятно

Пусть $\angle BFE = \alpha$, тогда $\angle BFE = \angle BEF = \angle MEA = \angle NFC = \alpha$. Заметим что $2AC = AB + BC$, пусть $BE = BF = x, AE = z, FC = y$, тогда $AC = AE + CF = z + y = (x + y + x +z)/2$, откуда $z + y = 2x$. По теореме синусов для треугольника $BEF$ получим $\frac{x}{\sin \alpha} = \frac{EF}{\sin (180^\circ - 2\alpha)} = \frac{EF}{\sin 2\alpha} = \frac{EF}{2\sin \alpha \cos \alpha}$, откуда $\frac{EF}{\cos \alpha} = 2x$. В треугольниках $MEA, CNF$ получим $\frac{ME}{\cos \alpha} = z$, $\frac{FN}{\cos \alpha} = y$ соответственно, откуда следует что $ME+ FN = EF$.