Математикадан республикалық олимпиада, 2020-2021 оқу жылы, 11 сынып
Сүйірбұрышты $ABC$ үшбұрышы $\Omega$ шеңберіне іштей сызылған. Осы үшбұрыштың $AD, BE$ және $CF$ биіктіктері жүргізілген. $AD$ түзуі $\Omega$--ны екінші рет $P$ нүктесінде, ал $PF$ және $PE$ түзулері $\Omega$--ны екінші рет сәйкесінше $R$ және $Q$ нүктелерінде қияды. $O_1$ және $O_2$ нүктелері сәйкесінше $BFR$ және $CEQ$ үшбұрыштарына сырттай сызылған шеңберлердің центрлері болсын. $O_1O_2$ түзуі $EF$ кесіндісінің ортасынан өтетінін дәлелдеңіз.
(
Шынтас Н.
)
посмотреть в олимпиаде
Комментарий/решение:
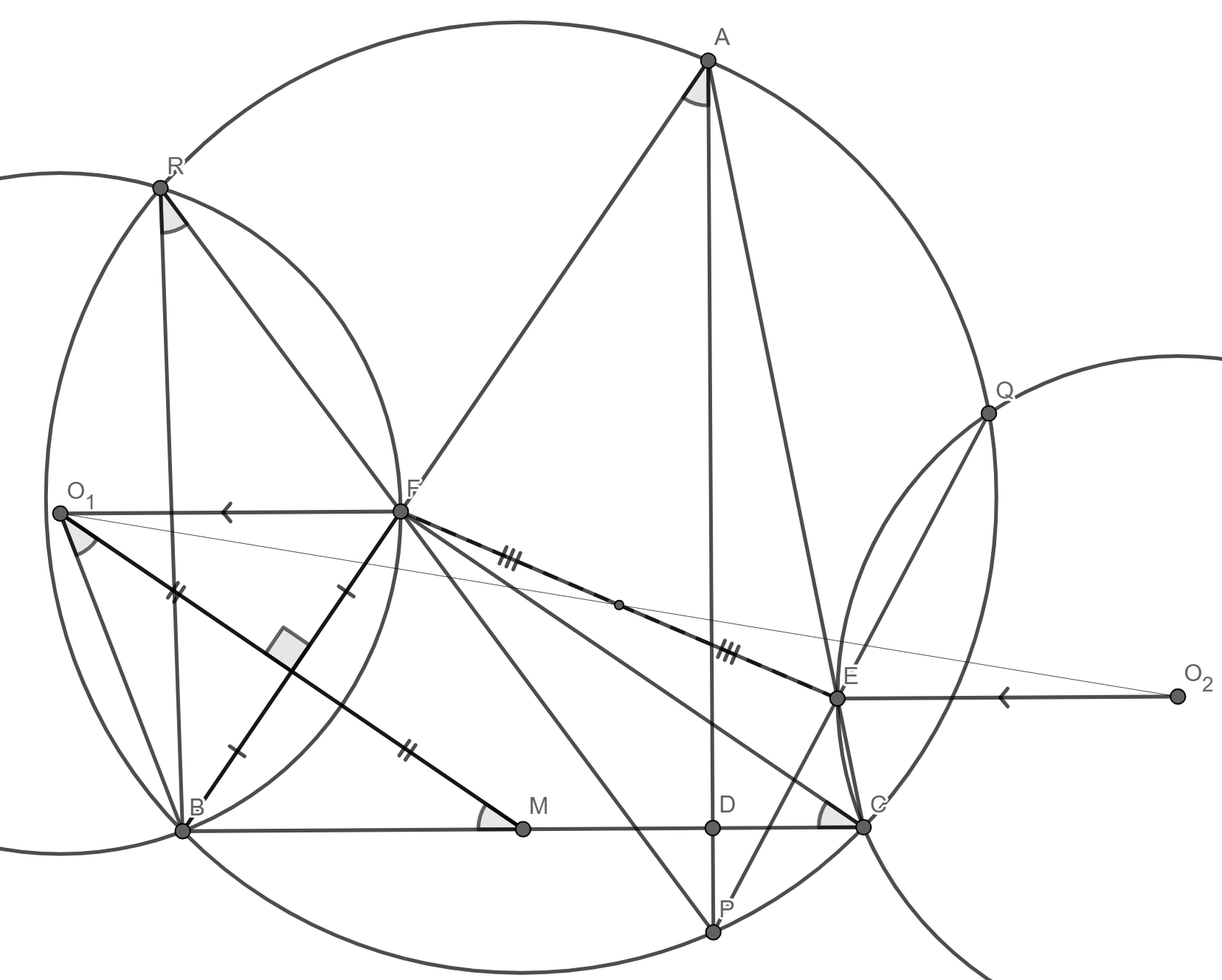
Комментарии от администратора Комментарии от администратора №1. Пусть $M$ середина $BC$. Так как $O_1B = O_1F$ и $MB = MF$, то $MO_1 \perp BF$. Следовательно, $MO_1 \parallel CF$. Заметим, что $$\angle BO_1M = \dfrac{\angle BO_1F}{2} = \angle BRF = \angle BRP = \angle BAP = {90}^{\circ} - \angle ABC = \angle BCF = BMO_1,$$ то есть четырехугольник $O_1FMB$ — ромб. Следовательно, $O_1F = BM$ и $O_1F \parallel BC$. Аналогично, $EO_2 = CM = BM$ и $EO_2 \parallel BC$. Значит, четырехугольник $O_1FO_2E$ — параллелограмм, то есть $O_1O_2$ делит $FE$ пополам.
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.