Азиатско-Тихоокеанская математическая олимпиада, 2019 год
Комментарий/решение:
Лемма 1: Пусть окружности $ω_1$ и $ω_2$ пересекаются в точках $W$ и $V$.
Если прямая проходящая через $W$ пересекает $ω_1$ и $ω_2$ в точках $M_1$ и $N_1$ соответственно,
а прямая проходящая через $V$ пересекает $ω_1$ и $ω_2$ в точках $N_1$ и $N_2$ соответственно, то $M_1N_1\parallel M_2N_2$ ;
Решение:
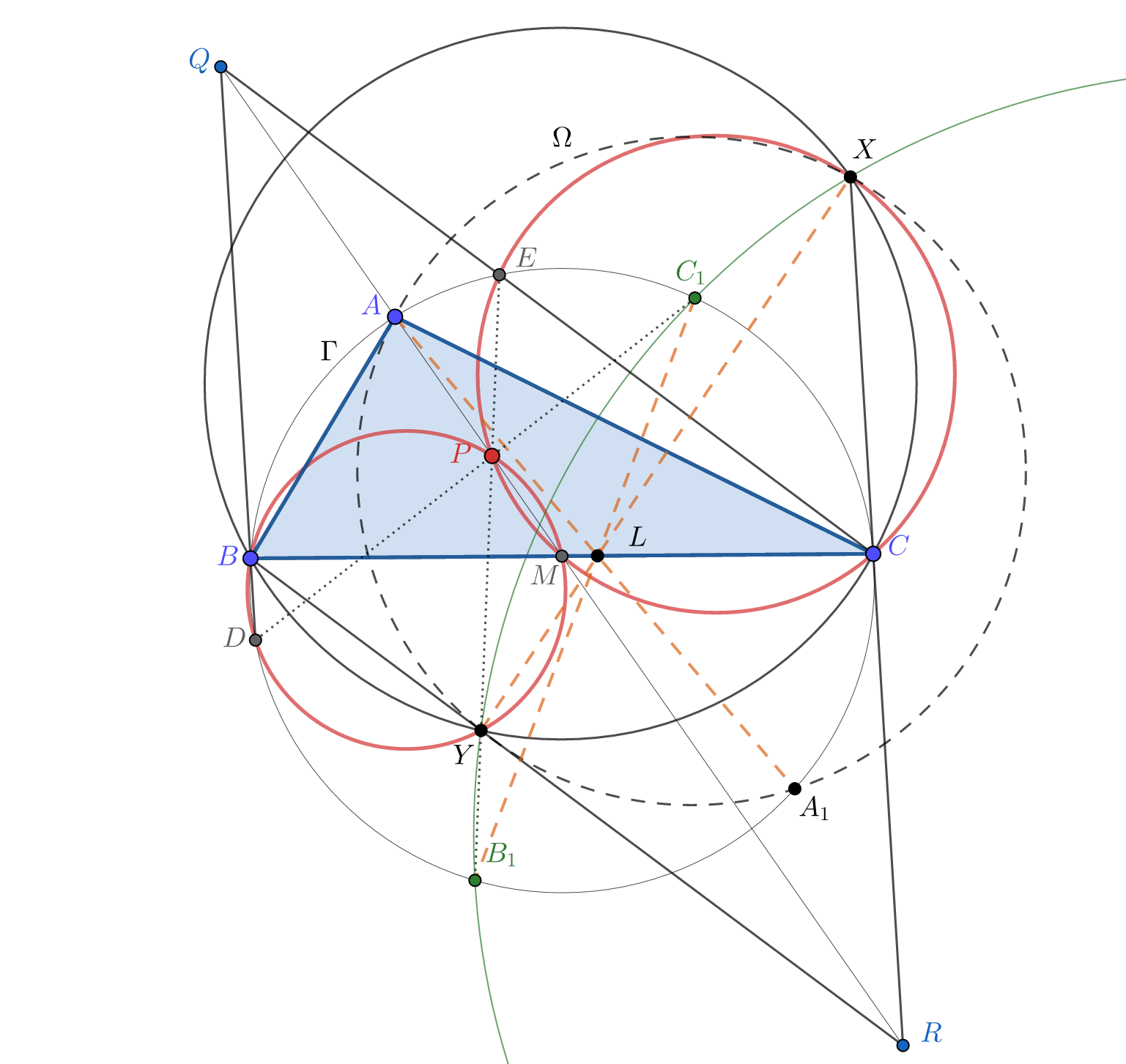
Пусть описанные окружности $\triangle BMP$, $\triangle CMP$ и $\triangle AXY,\quad$ $W_1$, $W_2$ и $Ω$ соответственно.
Заметим, что прямые $PM$, $DB$, $EC$ радикальные оси пар окружностей $W_1,W_2,Γ$, поэтому эти прямые пересекаются в одной точке, обозначим эту точку как $Q$.
Из Леммы 1 следует, что $BY\parallel EC$ и $CX\parallel DB$, так как $QM$ медиана $\triangle BQC$,
то $BY$, $CX$, $QM$ пересекаются в одной точке - $R$, при этом $BQCR$ - параллелограмм.
Заметим, что $R$ лежит на радикальной оси $W_1$ и $W_2$, откуда $$RY×RB=RX×RC$$
Значит точки $B,C,X,Y$ лежат на одной окружности - $ω$.
Пусть $(Ω\cap Γ)=A_1$. Тогда $AA_1$ радикальная ось окружностей $Ω$ и $Γ$.
Заметим, что $BC$ и $XY$ радикальные оси пар окружностей ($Γ$ , $ω$) и ($Ω$ , $ω$) соответственно.
Значит $AA_1, BC, XY$ пересекаются в одной точке - $L$.
Пусть $(EY\cap Γ)=B_1$ и $(DX\cap Γ)=C_1$, тогда из Леммы 1: $BB_1\parallel AM\parallel CC_1$,
откуда точки $B_1, C_1$ не зависят от выбора точки $P$.
Так как $BQCR$ - параллелограмм, то $$\frac{EP}{PY}=\frac{QP}{PR}=\frac{DP}{PX}$$
откуда $XY\parallel DE$, но так как $DE$ антипараллельна $B_1C_1$ относительно $\angle DPE$,
то $XY$ антипараллельна $B_1C_1$ относительно $\angle DPE$,
откуда точки $X,Y,B_1,C_1$ лежат на одной окружности $W$.
Легко заметить, что прямые $BC, XY, B_1C_1$ радикальные оси пар окружностей $Γ, ω, W$.
Значит $AA_1, BC, B_1C_1$ пересекаются в точке $L$,
но так как пересечение $BC$ и $B_1C_1$ не зависит от выбора точки $P$,
то точка $A_1$ не зависит от точки $P$,
откуда все окружности $Ω$ проходят через точку $A_1$ не зависящую от точки $P$.
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.