Азиатско-Тихоокеанская математическая олимпиада, 2018 год

Пусть $H$ является точкой пересечения высот треугольника $ABC$, $M$ и $N$ являются серединами сторон $AB$ и $AC$ соответственно. Пусть точка $H$ лежит внутри четырехугольника $BMNC$, а описанные окружности треугольников $BMH$ и $CNH$ касаются друг друга. Прямая, проходящая через точку $H$ и параллельная прямой $BC$, пересекает описанные окружности треугольников $BMH$ и $CNH$ в точках $K$ и $L$ соответственно. Пусть $F$ является точкой пересечения прямых $MK$ и $NL$, а $J$ является центром вписанной окружности треугольника $MHN$. Докажите, что $FJ = FA$. ( Mahdi Etesamifard )

Комментарий/решение

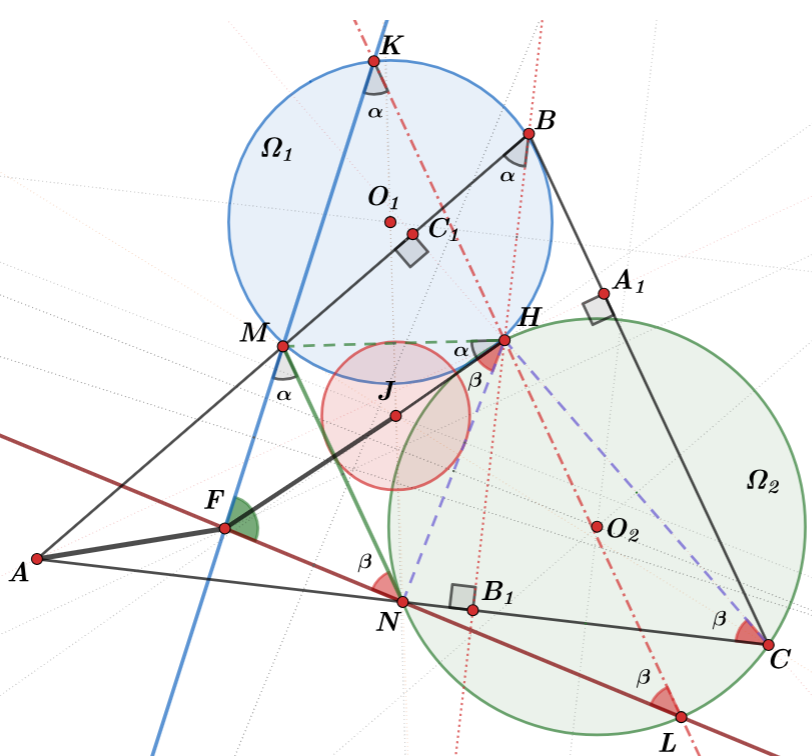
$$\triangleright \angle HKM =\angle HBM = \angle MHF=\alpha , \quad \angle NCH =\angle HLN =\angle FHN =\beta$$

$$ MN \parallel BC \parallel KL \Rightarrow \begin{cases} \angle MKH = \angle FMN=\alpha \\ \angle HLN = \angle MNF =\beta \end{cases}$$

$$ \angle MFN + \angle MHN = \pi \Rightarrow M,H,N,F \in \Omega_3$$

$$ \Omega_3: \angle FHN =\angle NMF \Rightarrow \alpha=\beta$$

$$ \Rightarrow FH \bot MN \Rightarrow \angle FMH =\angle FNH =90^o$$

$$ \angle MHF =\angle AMF =\alpha \qquad \angle NHF =\angle ANF =\alpha\Rightarrow$$

$$ A,N,M \in \Omega_4 : \quad AF=FN=FM =R_4\square $$

Так как H ортоцентр,$\angle ABH=\angle ACH=a$.$\angle BHC=90+a$.$\angle CBH=\angle BHK=\angle BMK=\angle AMF=b$.$\angle BCH=\angle LHC=\angle LNC=\angle ANF=c$.$90+a+b+c=90$.$a+b+c=180$.Заметим что $\angle FMN=\angle FNM=a$.$FM=FN$.Если проведём общую касательную то она будет биссектрисой угла $\angle MHN$ так как $\angle MBH=\angle NCH$.Значит $HJ$ и есть общая касательная и $\angle MHN=2a$.$\angle MJN=90+a$ так как $J$ инцентр $MHN$.$\angle MAN=b+c$ значит $MANJ$ вписанный четырёхугольник.$FM=FN$ и $\angle MFN=2\angle MAN$.Поэтому $F$ центр $(MAN)$ и $FA=FM=FN=FJ$.

Вашем решение вы не объяснили все подробно многие ди могут не понять этого так что прошу все подробно писать.

Вы просто переписали решение выше,с одной и той же идеей