Западно-Китайская математическая олимпиада, 2002 год
Дана трапеция $ ABCD$, в которой $ AD\parallel BC.$ Точка $ E$ движется по стороне $ AB.$ Пусть $ O_{1},O_{2}$ — центры описанных окружностей треугольников $ AED,BEC$, соответственно. Докажите, что длина отрезка $ O_{1}O_{2}$ постоянна.
посмотреть в олимпиаде
Комментарий/решение:
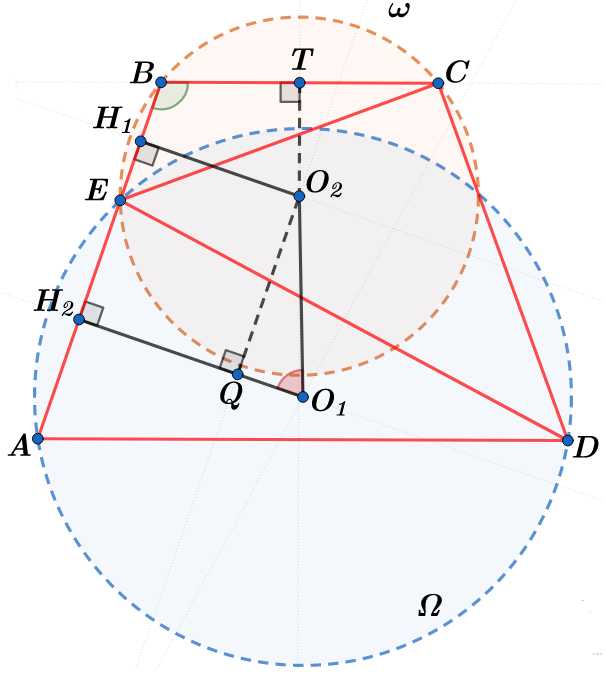
$$\omega: O_1H_1\bot EB , (H_1 \in AB) \Leftrightarrow BH_1=EH_1 \qquad \Omega:O_2H_2\bot AE, (H_2 \in AB) \Leftrightarrow AH_2=EH_2 $$
$$ \Rightarrow AB=2(EH_1+EH_2)=2H_1H_2 \Rightarrow H_1H_2=\frac{AB}{2}$$
$$ \square O_1H_2BT: \angle ABC +\angle H_2O_1T=\pi$$
$$ \square O_1H_2H_1O_2: O_2Q\bot H_2O_1 \Rightarrow O_2Q=H_1H_2=\frac{AB}{2}$$
$$ \triangle O_1O_2Q: O_1O_2=\frac{O_2Q}{\sin(\angle O_2O_1Q)}=\frac{AB}{2\sin(\angle ABC)}$$
$$O_1O_2=\frac{AB}{2\sin(\angle ABC)}=const$$

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.