1-я международная Иранская олимпиада по геометрии, 2014 год, первая лига

Дан прямоугольный треугольник с углами $\angle A=90^\circ$ и $\angle C=30^\circ$. Обозначим через $\Gamma$ окружность, проходящую через точку $A$ и касающуюся отрезка $BC$ в его середине. Пусть $\Gamma$ пересекает отрезок $AC$ в точке $N$, а описанную окружность $\triangle ABC$ во второй раз точке $M$. Докажите, что $MN \perp BC$.

Комментарий/решение

Решение максимально топорное, но ценителям координатного метода понравится )

1) Теорема :Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы

2) Непосредственно из (1) : $O\in BC;CO=BO=AO=R_{\Delta ABC}$

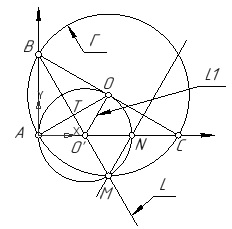
3) Введем систему координат как на рисунке

4) Если $BC=2a$, то координаты точек будут следующие:

$$A(0;0);C(2a\cdot\cos 30^\circ;0)\Rightarrow C(a\cdot\sqrt 3;0)$$

$$B(0;2a\cdot\sin 30^\circ)\Rightarrow B(0;a)$$

$$O\left(\dfrac{X_C}{2};\dfrac{Y_B}{2}\right)\Rightarrow O\left(\dfrac{a\sqrt 3}{2};\dfrac{a}{2} \right)$$

5) Пусть центр окружности $\Gamma$ это $O'$. Окружность $\Gamma$ касается точки $O$ и проходит через точку $A$. Это значит, что $OO'=O'A=R_{\Gamma}$, то есть, точка $O'$ равноудалена от точек $O$ и $A$

6) Теорема: Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре этого отрезка

7) Пусть $T$ - середина отрезка $AO$, тогда $T\left(\dfrac{a\sqrt 3}{4};\dfrac{a}{4} \right)$. Прямая $L$ (см рисунок) - серединный перпендикуляр для $AO$. Из (6) следует, что $O'\in L$

8) С другой стороны, точка $O$ - точка касания окружности $\Gamma$ и гипотенузы, а значит, центр окружности лежит на перпендикуляре к гипотенузе (прямая $L1$, см рисунок) в точке $O\Rightarrow O'\in L1$

9) Выпишем уравнения прямых $L$ и $L1$, решим систему, найдем координаты точки $O'$

$$L:A_L\cdot x + B_L \cdot y + CONST_L = 0$$

Нормаль к прямой $L$: $\overrightarrow{n_L} = (A_L;B_L)$ с одной стороны

С другой стороны $\overrightarrow{n_L} =2\cdot\overrightarrow{AO} =(a\sqrt3;a)$

$$L:a\sqrt3\cdot x + a \cdot y + CONST_L = 0$$

Для выяснения константы подставим точку $T$ в уравнение $L$

$$L:a\sqrt3\cdot \dfrac{a\sqrt3}{4} + a \cdot \dfrac{a}{4} + CONST_L = 0\Rightarrow CONST_L = -a^2$$

Окончательно уравнение $L$ с учетом сокращения всех коэффициентов на $a$

$$L:\sqrt3\cdot x + y -a = 0$$

10) Аналогичные действия для прямой $L1$

$$L1:A_{L1}\cdot x + B_{L1} \cdot y + CONST_{L1} = 0$$

Нормаль для $L1 : \overrightarrow{n_{L1}} =\overrightarrow{BC} =(a\sqrt3;-a)$

$$L1:a\sqrt3\cdot x -a \cdot y + CONST_{L1} = 0$$

Подставив точку $O$ в $L1$

$$L1:a\sqrt3\cdot\dfrac{a\sqrt3}{2} -a \cdot\dfrac{a}{2} + CONST_{L1} = 0\Rightarrow CONST_{L1} = -a^2$$

Окончательный вид уравнения $L1$

$$\sqrt3\cdot x - y -a = 0$$

11) Суммируя (9) и (10) имеем $2\sqrt3\cdot x = 2\cdot a \Rightarrow x_{O'}=\dfrac{a}{\sqrt 3};y_{O'}=0$

12) $AO' = O'N = R_{\Gamma}\Rightarrow x_N = 2x_{O'} = \dfrac{2a}{\sqrt 3};y_N = 0;$ Может возникнуть вопрос, почему $AO' =R_{\Gamma}$. Ответ - потому что $A$ - точка касания (обратите внимание, угол между радиусом и прямой $AB$ - прямой)

13) вычислим координаты точки $M$ из пересечения окружностей, ведь $M\in\Gamma$ и $M\in R_{\Delta ABC}$

$$\Gamma : (x-x_{O'})^2+y^2 = (AO')^2\Rightarrow \left(x-\dfrac{a}{\sqrt3}\right)^2+y^2 = \left(\dfrac{a}{\sqrt3}\right)^2$$

$$R_{\Delta ABC} : (x-x_{O})^2+(y-y_{O'})^2 = (BO)^2\Rightarrow \left(x-\dfrac{a\sqrt3}{2}\right)^2+\left(y-\dfrac{a}{2} \right)^2 = a^2$$

Решение системы: $x_M =\dfrac{a\sqrt3}{2} ;y_M =-\dfrac{a}{2}$

14) Если окажется, что скалярное произведение $\overrightarrow{MN}\cdot\overrightarrow{BC} = 0$, то это докажет, что $MN$ перпендикулярно гипотенузе (то есть то, что мы и доказываем)

$$\overrightarrow{MN} = (x_N-x_M;y_N-y_M)=\left(\dfrac{a}{2\sqrt3};\dfrac{a}{2}\right)$$

$$\overrightarrow{BC} = (x_C-x_B;y_C-y_B)=\left(a\sqrt3;-a\right)$$

$\overrightarrow{MN}\cdot\overrightarrow{BC} = \dfrac{a}{2\sqrt 3}\cdot a\sqrt3 + \dfrac{a}{2}\cdot (-a)=0 \forall a$

Проведем отрезок $DO$, перпендикулярный $BC$, где $D$ - середина $BC, O \in AC$. Заметим, что $O$ - центр $Г$, ведь точка $O$ лежит на пересечении серединного перпендикуляра к $AD$ с прямой $OD$. $\angle ACB=\angle AMB=30=\angle OAM, \angle NMA=90, \Rightarrow MN \perp BC$