Западно-Китайская математическая олимпиада, 2017 год

Пусть $D$ — точка на стороне $BC$ треугольника $ABC$. Точки $I_1$ и $I_2$ — центры вписанных окружностей треугольников $ABD$ и $ACD$ соответственно. Пусть $O_1$ и $O_2$ — центры описанных окружностей треугольников $AI_1D$ и $AI_2D$ соответственно. Также, пусть прямые $I_1O_2$ и $I_2O_1$ пересекаются в точке $P$. Докажите, что $PD\perp BC$.

Комментарий/решение

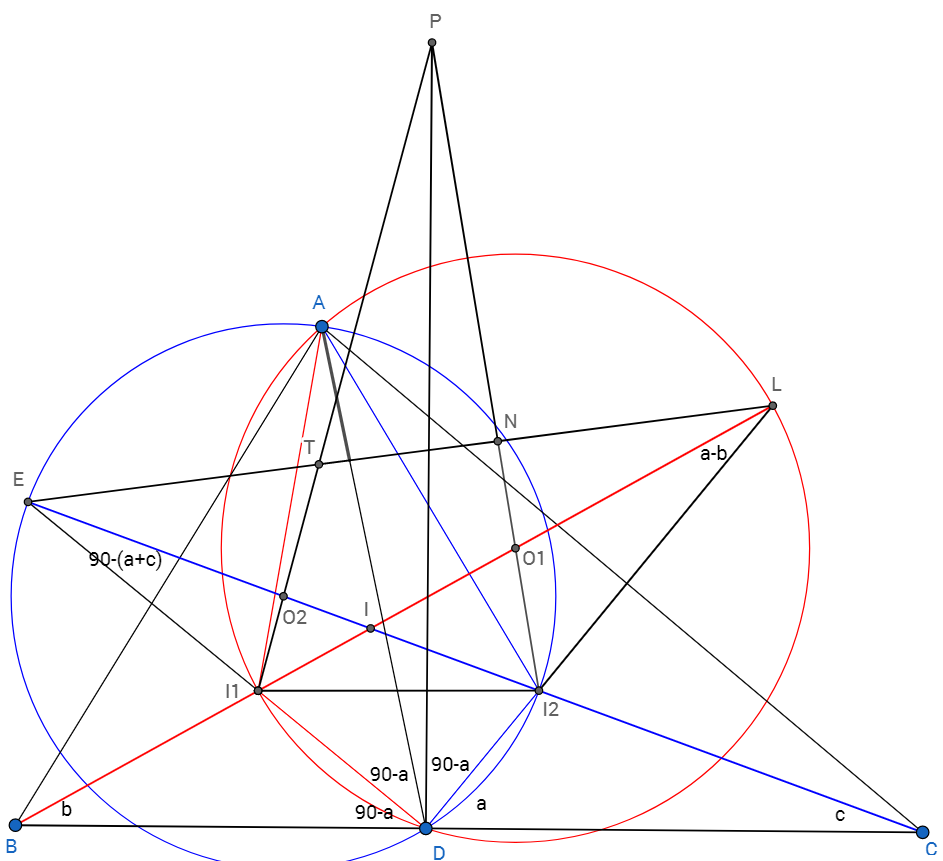
Пусть прямая $CI_{2}$ пересекает окружность с центром $O_{2}$ в точке $E$, $BI_{1}$ окружность с центром $O_{1}$ в точке $L$.

1)Покажем, что точки $C,\ I_{2}, \ O_{2}, \ E$ лежат на одной прямой. Обозначим углы $\angle ABC = 2b , \ \angle ACB = 2c, \ \angle ADC = 2a$ тогда $\angle I_{2}ED = \angle I_{2}AD = 90-(a+c)$, но $\angle I_{2}DE=90^{\circ}$ значит $\angle EI_{2}D = a+c$ с другой стороны $\angle DI_{2}C = 180-(a+c)$ значит $С, \ I_{2}, \ O_{2}, \ E$ лежат на одной прямой, аналогично и $B,\ I_{1}, \ O_{1}, \ L$ лежат на одной прямой.

2) Обозначим $T \in PI_{1} \cap LE$ и $N \in PI_{2} \cap LE$. Положим что $PD \perp BC$ тогда из этого следует, что $\angle ADE = \angle LDP$ откуда можно получить соотношение

$$\dfrac{\sin(\angle PI_{1}D)}{\sin(\angle PI_{2}D)} \cdot \dfrac{\sin(\angle PI_{2}I_{1})}{\sin(\angle PI_{1}I_{2})} \cdot \dfrac{\sin(\angle ADE)}{\sin(\angle ADL)}=1(*1)$$

так как $\dfrac{\sin(\angle PI_{1}D)}{\sin(\angle PI_{2}D)}=\dfrac{PI_{2}}{PI_{1}} \cdot tga$ , $\dfrac{\sin(\angle PI_{2}I_{1})}{\sin(\angle PI_{1}I_{2})}=\dfrac{PI_{1}}{PI_{2}}$ , $\dfrac{\sin \angle ADE }{\sin \angle ADL}=ctga$

3)Докажем $(*1)$

По теореме Менелая для $\Delta I_{2}EN, \ \Delta I_{1}LT$ и секущих $PO_{2}, \ PO_{1}$ соответственно получаем

$\dfrac{ET}{TN} \cdot \dfrac{PN}{PI_{2}}=1$ и $\dfrac{LN}{TN} \cdot \dfrac{PT}{PI_{1}}=1$ откуда $\dfrac{\sin(\angle PI_{2}I_{1})}{\sin(\angle PI_{1}I_{2})}=\dfrac{PI_{1}}{PI_{2}} = \dfrac{LN \cdot PT}{ET \cdot PN}(*)$

из $\Delta I_{1}ET , \ \Delta I_{2}NL$ в итоге получаем

$\dfrac{\sin(PI_{1}D)}{\sin(PI_{2}D)}=\dfrac{ET}{EI_{1}} \cdot \dfrac{LI_{2}}{LN} \cdot \dfrac{PN}{PT}(**)$

Умножая $(*)$ и $(**)$ и подставляя в $(1)$ получем $\dfrac{LI_{2}}{EI_{1}}=tga$

4) Осталось доказать что $\dfrac{LI_{2}}{EI_{1}}=tga$ в этом можно убедиться, выразив $EI_{1} , \ LI_{2}$ через треугольники $EDI_{2}, \ \ LDI_{1}$ , затем $DI_{1}, \ DI_{2}$ через $BD, \ CD$ затем через $AD$ получаем в итоге $LI_{2}=AD\cdot sina \cdot (tg(b)+tg(c))$ и $EI_{1} = AD \cdot cosa \cdot(tg(b)+tg(c))$ чтд.

5) Значит $(*1)$ верен и $PD \perp BC$.