3-я международная Иранская олимпиада по геометрии, 2016 год, первая лига, 7-8 классы

Вокруг треугольника $ABC$ $(AC>AB)$ описана окружность $\omega$. На стороне $AC$ и на окружности $\omega$ выбрали точки $X$ и $Y$ соответственно так, что $CX=CY=AB$. При этом точки $A$ и $Y$ лежат по разные стороны от прямой $BC$. Прямая $XY$ пересекает окружность $\omega$ второй раз в точке $P$. Докажите, что $PB=PC$.

Комментарий/решение

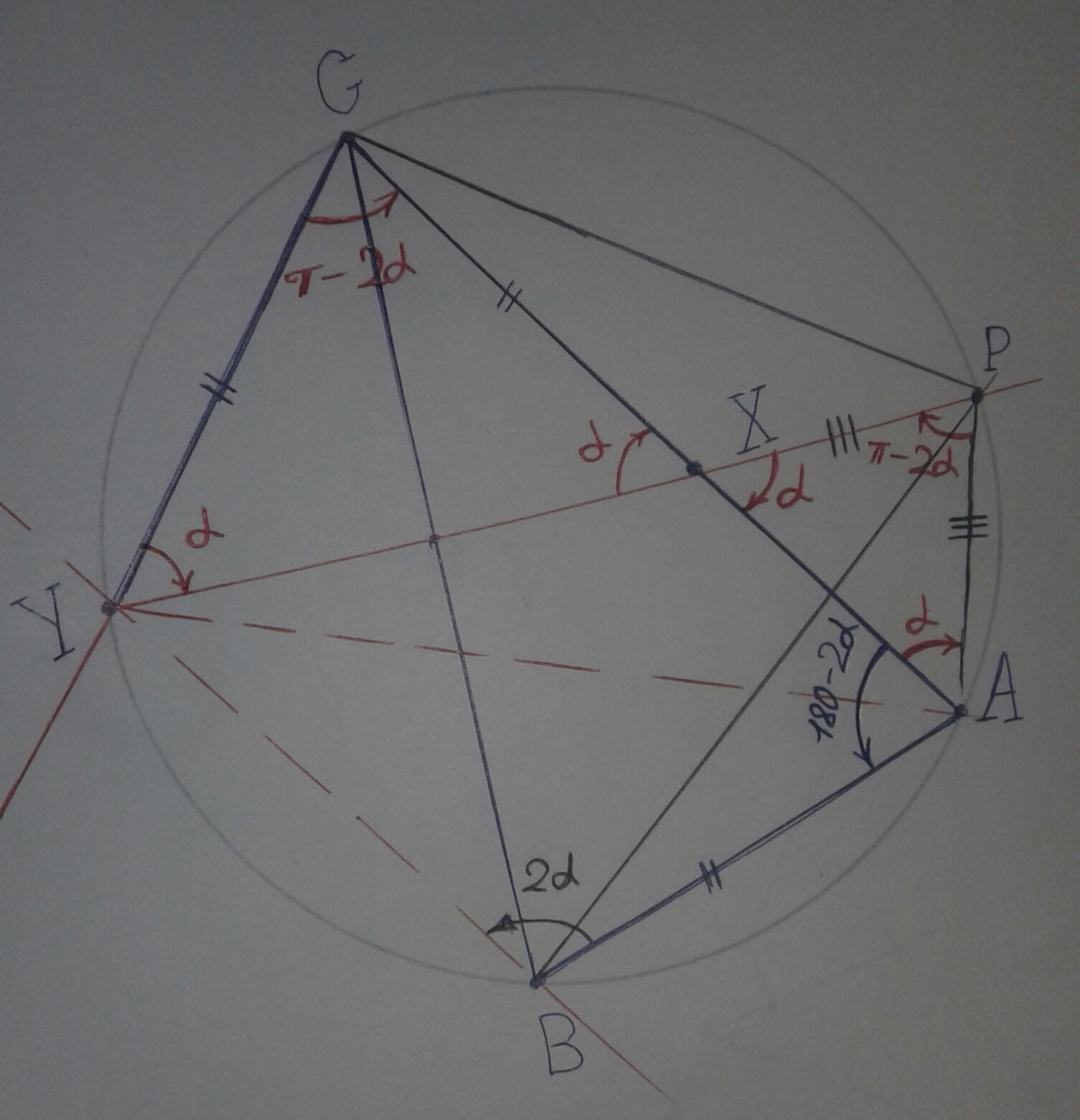
$$\triangle {CXY}: CX=CY \Rightarrow \angle CYX= \angle CXY=\alpha.$$

$$\omega: \angle CYP =\angle CAP=\alpha.$$

$$CA \cap CP \Rightarrow \angle CXY = \angle PXA=\alpha.$$

$$\triangle{XPA}: \angle PXA= \angle PAX=\alpha \Rightarrow XP=PA.$$

$$CY=AB \Rightarrow \breve{YC}=\breve{AB} \Rightarrow AC \parallel BY \Rightarrow \angle YCA= \angle CAB= \pi- 2\alpha.$$

$$\triangle {PAB}: \angle PAB=\angle BAC+ \angle CAP= \pi - \alpha.$$

Тогда $\angle PYB = 180^\circ-\angle PAB=\alpha.$ Так как $\angle CYP = \angle BYP = \alpha$, то $CP=BP.$