Республиканская олимпиада по математике, 2016 год, 9 класс
Комментарий/решение:
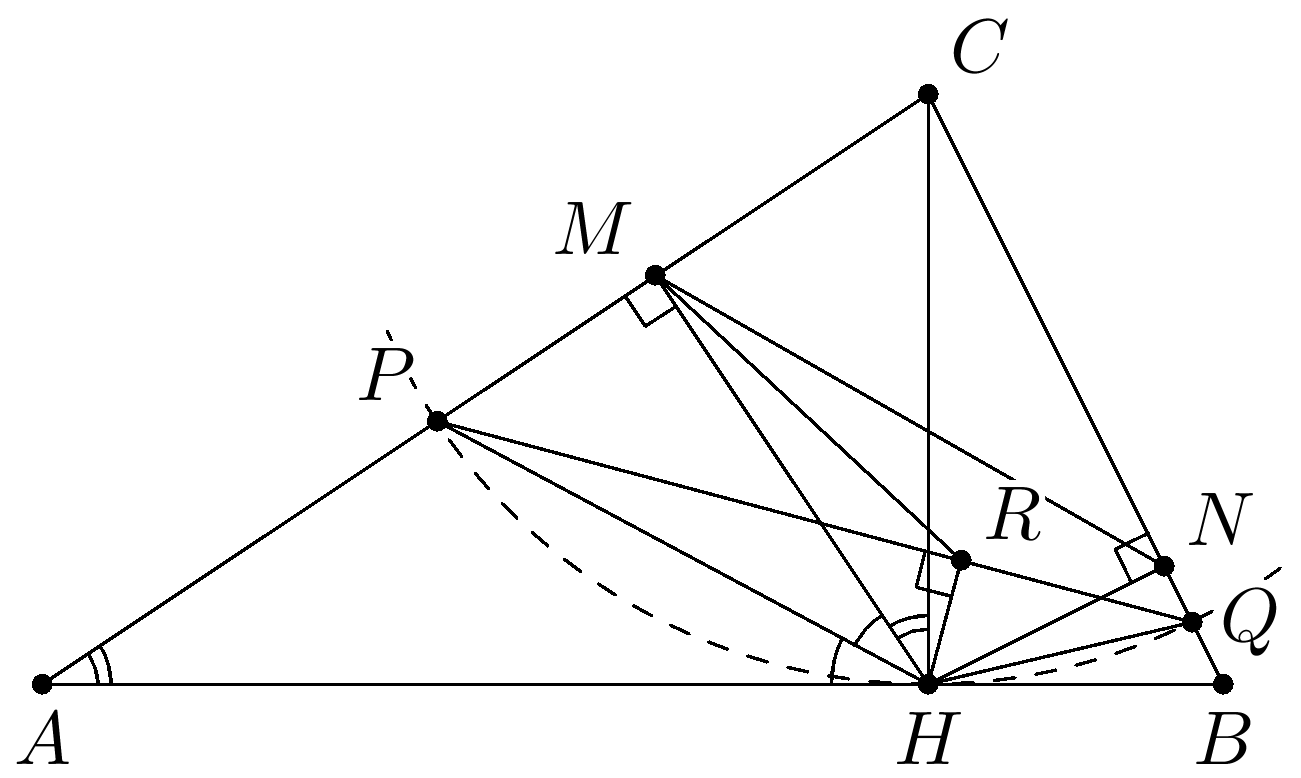
Комментарии от администратора Комментарии от администратора №1. Заметим, что $\angle CHM = \angle HAC$. Обозначим эти углы через $\alpha$. Тогда в треугольнике $AHP$ внешний угол при вершине $P$ состоит из угла $\alpha$ и половины угла $AHM$, и угол $\angle CHP$ состоит из тех же углов. Следовательно, $\angle CHP = \angle CPH$ или $CH=CP$. Аналогично $CH=CQ$. Значит, можно провести окружность с центром в точке $C$ радиусом $CH$. Из того, что четырехугольник $CMHN$ вписанный и точки $P$, $M$, $R$ и $H$ лежат на одной окружности с диаметром $PH$, следует, что $\angle RMH = \angle RPH = \angle NCH/2 = \angle NMH$. Следовательно, угол $RMH$ в два раза меньше угла $NMH$, то есть $MR$ делит угол $NMH$ пополам. Аналогично, $NR$ делит угол $MNH$ пополам, то есть $R$ — точка пересечения биссектрис треугольника $MNH$.
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.