Республиканская олимпиада по математике, 2016 год, 11 класс

Две пересекающиеся в точках $X$ и $Y$ окружности $\omega_1$ и $\omega_2$ находятся внутри окружности $\Omega$ и касаются ее в точках $A$ и $B$. Прямая $AB$ повторно пересекает окружности $\omega_1$ и $\omega_2$ в точках $A_1$ и $B_1$, соответственно. Вписанная в криволинейный треугольник $A_1B_1X$ окружность касается стороны $A_1B_1$ в точке $Z$. Докажите, что $\angle AXZ=\angle BXZ$.

( Ильясов С. )

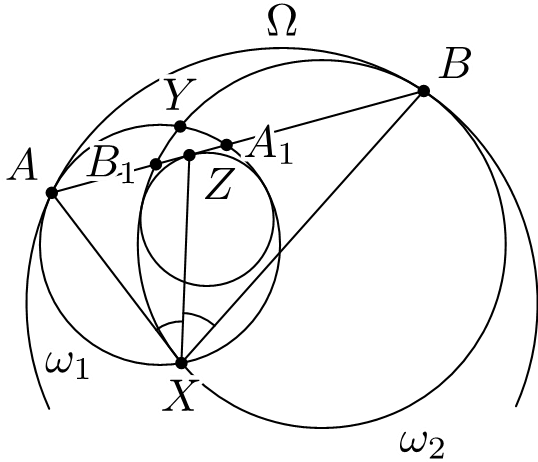
Комментарий/решение

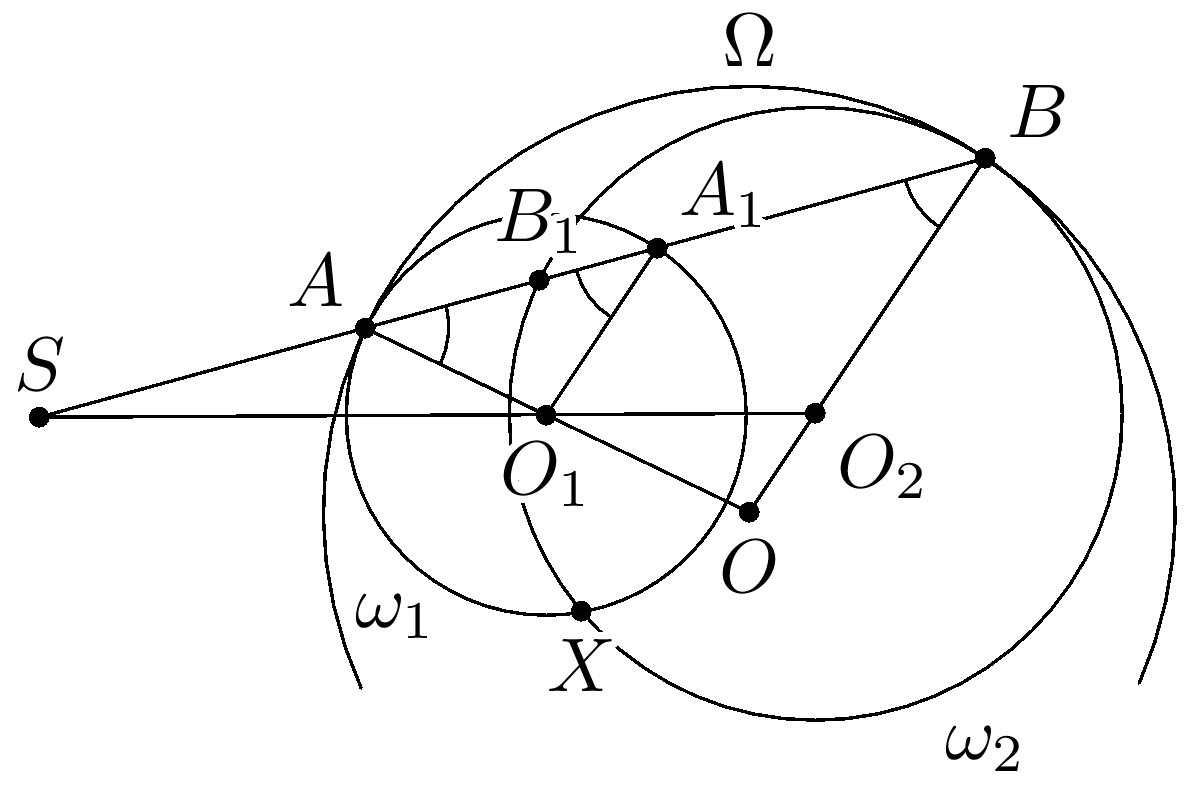
Комментарии от администратора Комментарии от администратора №1.     Пусть $O_1$ и $r_1$ соответственно центр и радиус $\omega_1$, а $O_2$ и $r_2$ соответственно центр и радиус $\omega_2$. Пусть $\omega$ — вписанная окружность в криволинейного треугольника $A_1B_1X$, а $I$ — ее центр. Точку касания окружностей $\omega$ и $\omega_1$ обозначим через $P$, а окружностей $\omega$ и $\omega_2$ через $Q$. Пусть $AB \cap O_1O_2=S$. Легко заметить, что $\angle O_2BA = \angle O_1AB = \angle O_1A_1A$, то есть $O_1A_1 \parallel OB$. Тогда $S$ — центр гомотетии, переводящий $\omega_1$ в $\omega_2$, с коэффициентом $r_1/r_2$.
Теперь, обозначим $PQ \cap O_1O_2 =S'$. И пусть $PQ$ во второй раз пересекает $\omega_2$ в точке $Q_1$. Тогда $\angle O_2Q_1Q = \angle IQP = \angle QPI$, то есть $O_1P \parallel O_2Q_1$. Как видим, точка $S'$ также является центром гомотетии, переводящий $\omega_1$ в $\omega_2$ с положительным коэффициентом $r_1/r_2$. Следовательно, $S$ и $S'$ совпадают. Значит, $AB \cap PQ \cap O_1O_2 =S$.

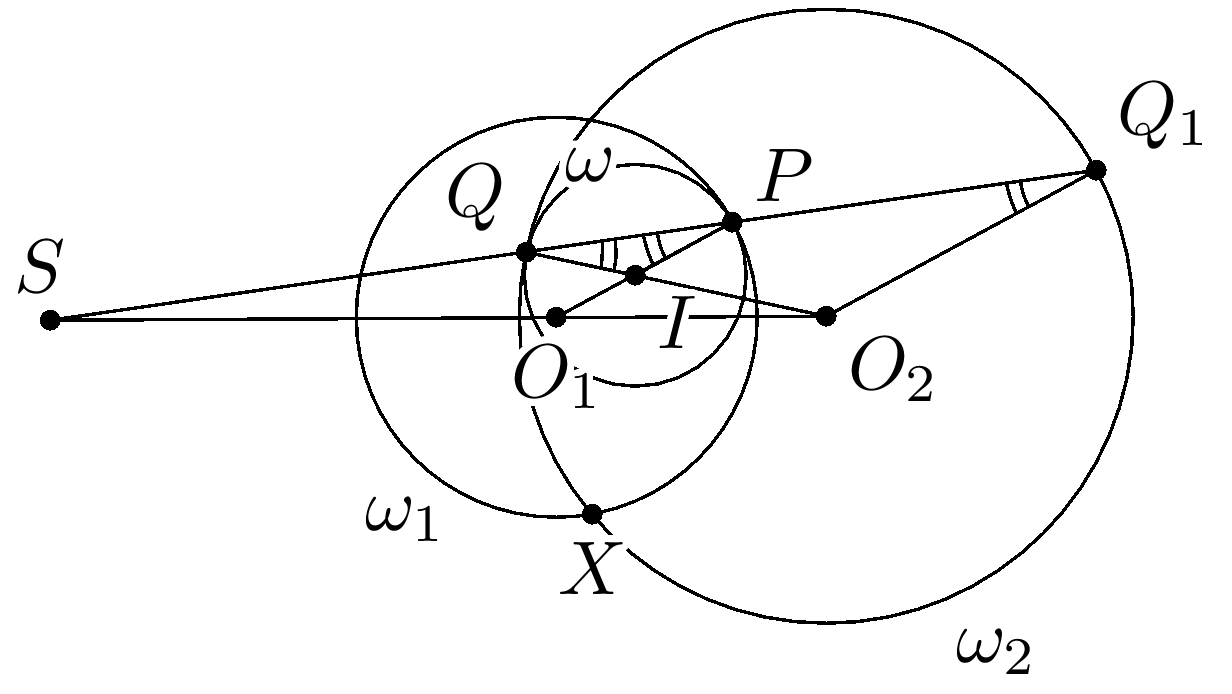
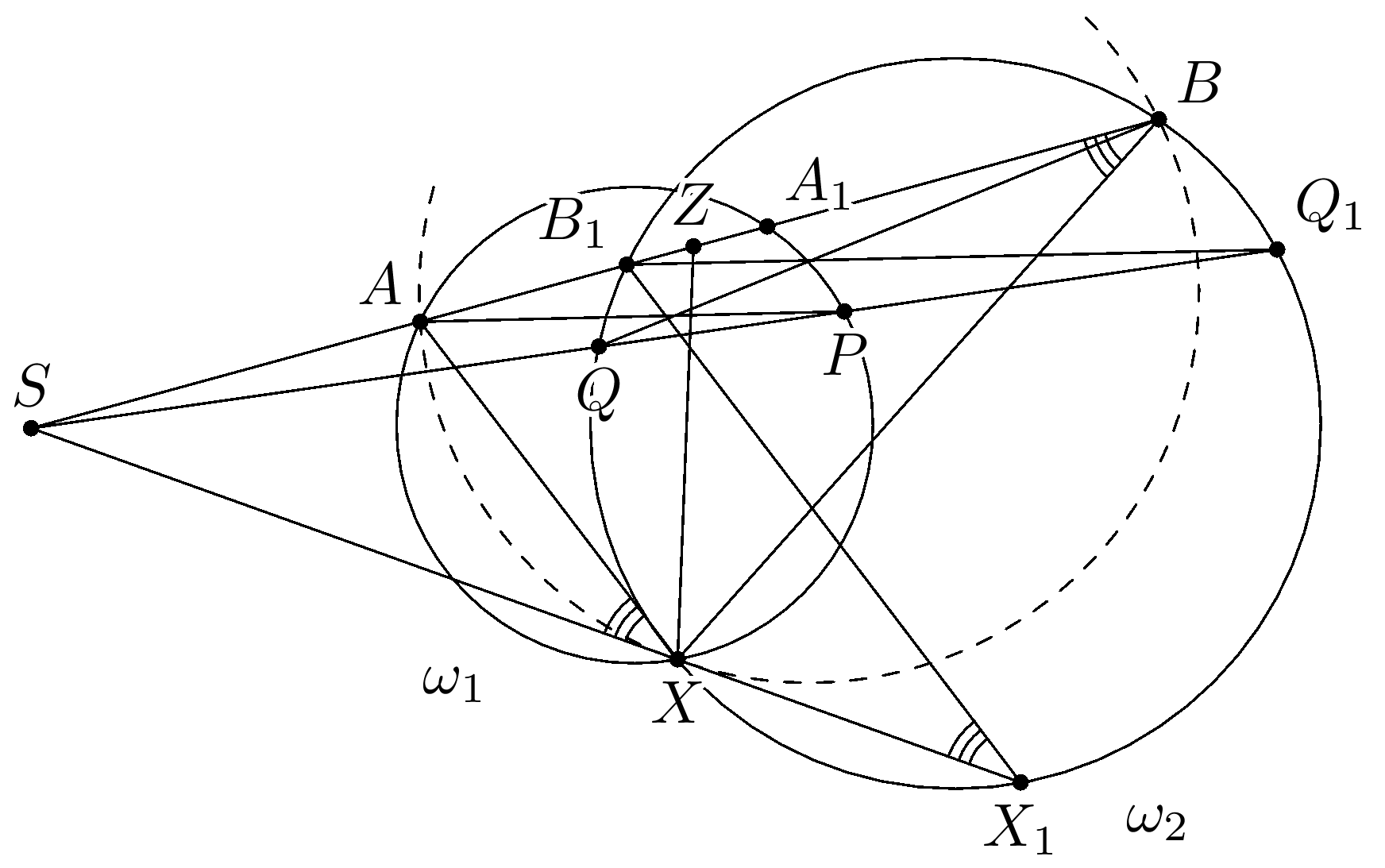
Доказать, что $SZ$ $=$ $SX$ можно по-другому.

Как и в указанном выше решении пользуемся тем фактом, что прямые $AB$ и $PQ$ пересекаются в центре гомотетии $S$, переводящей окружности $\omega_1$ в $\omega_2$.

Для этого рассмотрим инверсию $F$ с радиусом $\sqrt{SA \cdot SB}$ и центром в точке $S$. Ясно что такая инверсия переводит окружность $\Omega$ саму в себя. Далее, поскольку $\frac{SA}{SA_1}$ $=$ $\frac{SB_1}{SB}$, то $SA \cdot SB$ $=$ $SA_1 \cdot SB_1$. Это значит, что окружность $\omega_1$, проходящая через точки $A$ и $A_1$ и касающаяся окружности $\Omega$ в точке $A$ перейдет в окружность, проходящую через точки $B$ и $B_1$ и касающуюся $\Omega$ в точке $B$, то есть в окружность $\omega_2$ (Причем внешние дуги ($XAY$ и $XBY$) соответствующих окружностей перейдут друг в друга, а внутренняя дуга $XA_1Y$ в дугу $XB_1Y$). Что влечет за собой, то что точки $P$ и $Q$ перейдут друг в друга, а точка $X$ сама в себя.

Итак, инверсия $F$ меняет местами окружности $\omega_1$,$\omega_2$ и точки $P$ и $Q$. Это говорит о том, что инверсия $F$ переводит окружность $\omega$ саму в себя. Осталось заметить, что образ прямой $AB$ есть прямая $AB$, поэтому точка касания $Z$ прямой $AB$ и окружности $\omega$ останется на месте при инверсии $F$ (как и точка $X$), стало быть $SX$ $=$ $SZ$.