Олимпиада Туймаада по математике. Старшая лига. 2011 год

Окружности $\omega_1$ и $\omega_2$ пересекаются в точках $A$ и $B$, точка $M$ — середина $AB$. На прямой $AB$ выбраны точки $S_1$ и $S_2$. Касательные, проведенные из $S_1$ к окружности $\omega_1$ касаются ее в точках $X_1$ и $Y_1$, а касательные из $S_2$ к $\omega_2$ касаются ее в точках $X_2$ и $Y_2$. Докажите, что если прямая $X_1X_2$ проходит через $M$, то прямая $Y_1Y_2$ тоже проходит через $M$. ( А. Акопян )

Комментарий/решение

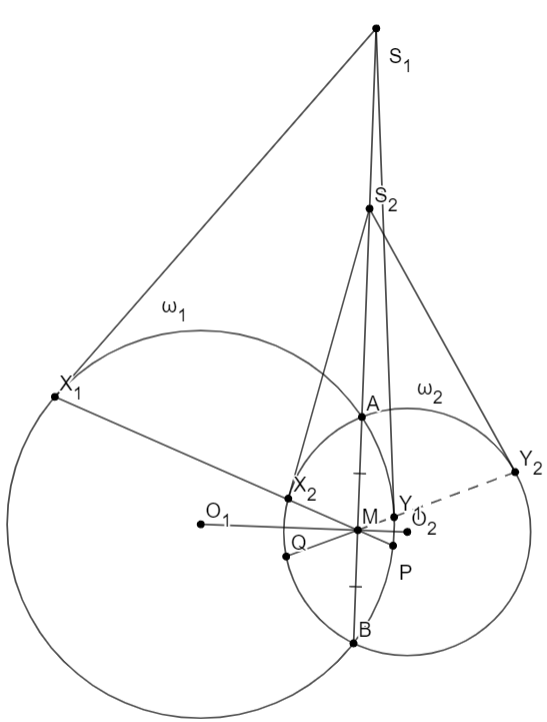
$O_1,O_2$ - центры $\omega_1,\omega_2$ соответственно.

Утверждение:

$P = X_1M \cap \omega_1,$ тогда $P$ - точка симметричная $Y_1$ относительно $O_1O_2$, $Q = Y_2M \cap \omega_2$, тогда $Q$ симметрична $X_2$ относительно

$O_1O_2$.

Доказательство:

$AX_1BY_1$ и $AX_2BY_2$ - гармонические четырехугольники, тогда раз двойные отношения сохраняются при проецировании с окружности на прямую, имеем:

$$(A,X_1;B,Y_1) \stackrel{P}{=} (A,M;B, \infty), (A,X_2;B,Y_2) \stackrel{Q}{=} (A,M;B, \infty)$$

Это доказывает, что $PY_1||AB||QX_2$, а значит $P$ симметрична $Y_1$ относительно $O_1O_2$, $Q$ симметрична $X_2$ относительно $O_1O_2$., тогда получаем трапецию $Y_1X_2QP$, где $M$ лежит на диагонали $X_2P$, а также на отрезке соединяющем середины оснований $X_2Q, Y_1P$, то есть, по замечательному свойству трапеции $M$ лежит и на диагонали $Y_1Q$, что и есть прямая $Y_1Y_2$.