Городская олимпиада «Аль-Фараби» по математике, 10-11 классы
Какое наибольшее количество ферзей можно поставить на шахматную доску так, чтобы каждый из них бил не более двух других? (Фигуры не бьют друг сквозь друга.)
посмотреть в олимпиаде
Комментарий/решение:
Это предпросмотр
Комментарии от администратора Комментарии от администратора №1. Ответ: 14. Пример расстановки показан на рисунке ниже.
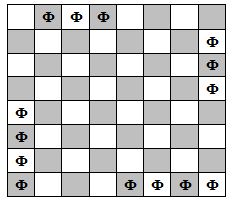
Докажем, что нельзя поставить 15 ферзей. Каждый ферзь бьет в восьми направлениях, причем лишь в двух из них он может бить других ферзей, значит, как минимум в 6 направлениях он бьет за пределы доски. На доске есть $2\times 8\times 2+2\times 15\times 2=94$ возможных направления удара за пределы доски. Если бы удалось поставить 15 ферзей, они вместе били бы за пределы доски не менее чем в 90 направлениях. Так как ферзи не могут стоять во всех четырех угловых клетках доски (поскольку бьют друг друга), они занимают не более трех угловых клеток. Если ферзи стоят в трех углах, то найдутся хотя бы две диагонали длины 2, на которых нет ферзей, тогда общее число возможных направлений будет не более 88 (поскольку в такой расстановке не реализованы удары ферзей для 6 диагональных направлений — двух у четвертой угловой клетки и двух у каждой короткой диагонали). Если занято только два угла, то все равно найдется диагональ длины 2 без ферзя, поэтому и в этом случае получается не более 88 направлений. Наконец, если три угла свободны, то и в этом случае получается не более 88 направлений. Значит, 15 ферзей так расположить невозможно.

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.