Городская Жаутыковская олимпиада, 7 класс, 2007 год
Комментарий/решение:
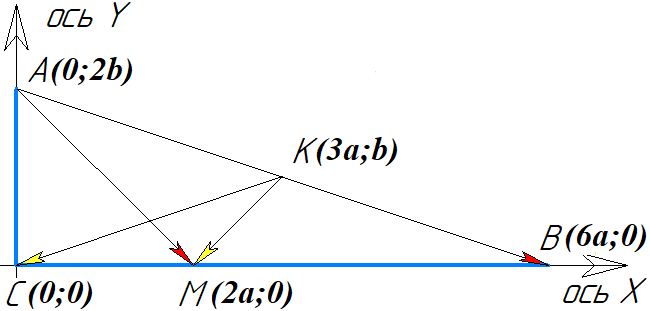
$\cos {\angle MAB}=\angle (\overrightarrow{AM},\overrightarrow{AB})=\dfrac {\overrightarrow{AM} \cdot {\overrightarrow{AB}}}{\overrightarrow{|AM|} \cdot {\overrightarrow{|AB|}}}$
$\cos {\angle MKC}=\angle (\overrightarrow{KM},\overrightarrow{KC})=\dfrac {\overrightarrow{KM} \cdot {\overrightarrow{KC}}}{\overrightarrow{|KM|} \cdot {\overrightarrow{|KC|}}}$
$\overrightarrow{AM}=(2a;-2b);\overrightarrow{AB}=(6a;-2b);\overrightarrow{KM}=(-a;-b);\overrightarrow{KC}=(-3a;-b) $
$\overrightarrow{|AM|}=\sqrt{(2a)^2+(-2b)^2}=2\cdot{\sqrt{a^2+b^2}};$
$\overrightarrow{|AB|}=\sqrt{(6a)^2+(-2b)^2}=2\cdot{\sqrt{(9a)^2+b^2}};$
$\overrightarrow{|KM|}=\sqrt{a^2+b^2};$
$\overrightarrow{|KC|}=\sqrt{(9a)^2+b^2};$
$\overrightarrow{AM} \cdot {\overrightarrow{AB}}=2a\cdot {6a}+(-2b)\cdot {(-2b)}=12a^2+4b^2$
$\overrightarrow{KM} \cdot {\overrightarrow{KC}}=(-a)\cdot {(-3a)}+(-b)\cdot {(-b)}=3a^2+b^2$
Осталось сравнить $\cos {\angle MAB}$ и $\cos {\angle MKC}$
$\cos {\angle MAB}=\angle (\overrightarrow{AM},\overrightarrow{AB})=\dfrac {12a^2+4b^2}{4\cdot{\sqrt{a^2+b^2}}\cdot{\sqrt{9a^2+b^2}}}$
$\cos {\angle MKC}=\angle (\overrightarrow{KM},\overrightarrow{KC})=\dfrac {3a^2+b^2}{\cdot{\sqrt{a^2+b^2}}\cdot{\sqrt{9a^2+b^2}}}$
Получили равные выражение, то есть $\angle MAB=\angle MKC$
PS. Это просто один из возможных вариантов решения. Я понимаю, что он явно не соответствует программе семиклассника. Скалярное произведение знают школьники 10-11 класса.
Теорема LTE для 10 классов-норм
Функциональные уравнения для 11 классов -норм
Малая теорема Ферма для 9 класса-норм
И это ещё не самое сложное, предлагаемое на Районных этапах олимпиад.
Так почему скалярное произведение, где нужно уметь складывать и умножать числа-не норм?
Я этого не понимаю
Так как $CK$- медиана то $CK=KB$ пусть $M'$ середина $BM$ тогда $BM'=MM'=CM$ так как $CK=BK$ то $M'$ симметрична относительно высоты $KH$ треугольника $BKC$, где $H \in BC$ тогда $KM' = \dfrac{AM}{2}$ как средняя линия и $\angle MKC = \angle M'KB = \angle MAB$

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.