Районная олимпиада, 2014-2015 учебный год, 10 класс


В квадрате $ABCD$ вершина $A$ и середина стороны $CD$ симметричны относительно прямой $l$. Найдите отношение площадей частей, на которые прямая $l$ делит квадрат $ABCD$.
посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1.     Ответ: Отношение площади меньшей части к большей равно $\frac{3}{5}$.
Решение. Пусть сторона квадрата равна 4, а вершины квадрата на координатной плоскости имеют координаты $A(0,0)$, $B(0,4)$, $C(4,4)$ и $D(4,0)$.

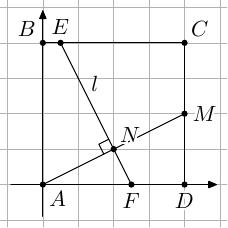
Если $M$ — середина $CD$, а $N$ — середина $AM$, то их координаты равны $M(4,2)$ и $N(2,1)$. Так как угловой коэффициент прямой $AM$ равен $1/2$, а прямая $l$ перпендикулярна $AM$, то ее угловой коэффициент равен $k_l=-2$. Зная угловой коэффициент прямой $l$ и точку, через которую она проходит, нетрудно найти ее уравнение: $-2x-y=-5$. Пусть $l$ пересекает прямую $BC$ в точке $E$, прямую $AD$ в точке $F$. Тогда координаты этих точек равны $E\left( {0,\!5,4} \right),F\left( {2,\!5,0} \right)$. Тогда площадь трапеции $ABEF$ равна $S_{ABEF}=4(0,\!5+2,\!5)/2=6$, а площадь трапеции $ECDF$ равна $S_{ECDF}=4(3,\!5+1,\!5)/2=10$, откуда и следует ответ.