Олимпиада имени Леонарда Эйлера2011-2012 учебный год, I тур заключительного этапа
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1. Решение. Предъявим пример таких многоугольников. Пусть многоугольник $M = A_1A_2 \dots A_{51}$ таков, что $A_1A_2 = A_2A_3 = \dots = A_{50}A_{51}$ и $\angle A_1A_2A_3 = \angle A_2A_3A_4 = \dots = \angle A_{49}A_{50}A_{51} = 179^\circ$. Построим треугольник $A_1A_{51}B$, содержащий $M$ и такой, что $\angle A_50A_51B = 1^\circ$ а $\angle BA_1A_2 > 1^\circ$. Мы утверждаем, что $M$ и $N = BA_1A_2 \dots A_{51}$ — пара требуемых многоугольников. $M$ и $N$ в объединении дают треугольник. Чтобы получить $(2k+1)$-угольник (при $2 \leq k \leq 49$), повернём $M$ так, чтобы отрезок $A_kA_{k+1}$ перешёл в отрезок $A_1A_2$; обозначим полученный многоугольник через $M' = C_1 \dots C_{51}$. Тогда в объединении многоугольники $M'$ и $N$ дадут многоугольник $BC_kC_{k - 1} \dots C_1A_{52 - k}A_{53 - k} \dots A_{51}$ с $2k+1$ вершиной. Чтобы получить $2k$-угольник (при $2 \leq k \leq 50$), повернём $M$ так, чтобы отрезок $A_1A_2$ перешёл в отрезок $A_kA_{k+1}$; обозначим полученный многоугольник через $M'' = D_1 \dots D_{51}$. Тогда точка $D_{52 - k} = A_{51}$ окажется на отрезке $D_{53 - k}B$, поэтому в объединении многоугольники $M''$ и $N$ дадут многоугольник $BA_1A_2 \dots A_kD_{51}D_{50} \dots D_{53 - k}$ с $2k$ вершинами. На рисунках показано, как получаются 3-, 7- и 6-угольники.
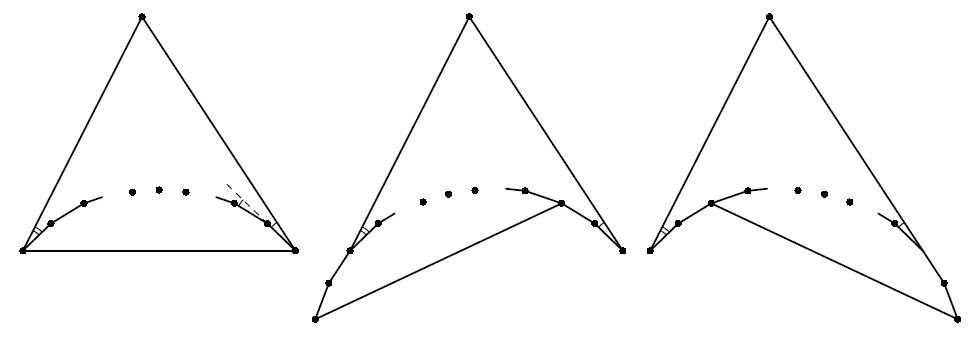
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.