А. Антропов
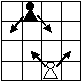
Есеп №1. $9 \times 9$ тор көзді тақтаға ең көп дегенде бір бірін жемейтіндей(сондай ақ, өзінің түсімен бірдей пешканы) қанша қара және ақ пешка қоюға (пешка, өзінің түсіне тәуелсіз кез келген шаршыға қоюға болады) болады? Ақ пешка нөмері үлкен көршіес екі диоганальді жейді, ал қара пешка нөмері төмен екі көршілес диоганальді жейді (сур. қараңыз).
комментарий/решение(1) олимпиада
Есеп №2. $ABC$ үшбұрышының $AB$ қабырғасы $BC$ қабырғасынан үлкен. $BC$ қабырғасының $C$ нүктесінен әрі қарай созындысынан $2BN=AB+BC$ болатындай $N$ нүктесін белгілеген. $BS$ — $ABC$ үшбұрышының биссектрисасы, $M$ — $AC$ қабырғасының ортасы, ал $L$ нүктесі $BS$ кесіндісіндегі $ML \parallel AB$ болатындай нүкте. $2LN=AC$ екенін дәлелдеңіздер. ( А. Антропов )
комментарий/решение(2) олимпиада
Есеп №3. а стороне $AB$ треугольника $ABC$ выбрана точка $P$, а на сторонах $AC$ и $BC$ точки $S$ и $T$ таким образом, что $AP=AS$ и $BP=BT$. Описанная окружность треугольника $PST$ вторично пересекает стороны $AB$ и $BC$ в точках $Q$ и $R$ соответственно. Прямые $PS$ и $QR$ пересекаются в точке $L$. Докажите, что прямая $CL$ делит отрезок $PQ$ пополам. ( А. Антропов )
комментарий/решение(1) олимпиада